Giải Bài 5 trang 106 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST

Lời giải chi tiết

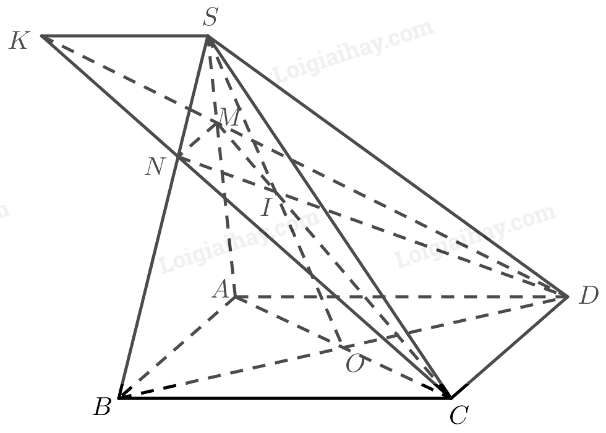
a) • Ta có:

\(\begin{array}{l}\left. \begin{array}{l}M \in \left( {IC{\rm{D}}} \right)\\M \in SA \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow M \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\\\left. \begin{array}{l}I \in \left( {IC{\rm{D}}} \right)\\I \in SO \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow I \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\\C \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\end{array}\)

\( \Rightarrow M,I,C\) thẳng hàng.

Do đó \(M\) là giao điểm của \(IC\) và \(SA\).

• Ta có:

\(\begin{array}{l}\left. \begin{array}{l}N \in \left( {IC{\rm{D}}} \right)\\N \in SB \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow N \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\\\left. \begin{array}{l}I \in \left( {IC{\rm{D}}} \right)\\I \in SO \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow I \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\\D \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\end{array}\)

\( \Rightarrow N,I,D\) thẳng hàng.

Do đó \(N\) là giao điểm của \(I{\rm{D}}\) và \(SB\).

• Ta có:

\(\begin{array}{l}AB = \left( {SAB} \right) \cap \left( {ABC{\rm{D}}} \right)\\C{\rm{D}} = \left( {IC{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\MN = \left( {SAB} \right) \cap \left( {IC{\rm{D}}} \right)\\AB\parallel C{\rm{D}}\end{array}\)

Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(AB\parallel C{\rm{D}}\parallel MN\).

Áp dụng định lí Medelaus cho tam giác \(SOA\) với cát tuyến \(CIM\), ta có:

\(\frac{{SM}}{{MA}}.\frac{{AC}}{{OC}}.\frac{{OI}}{{SI}} = 1 \Leftrightarrow \frac{{SM}}{{MA}}.2.1 = 1 \Leftrightarrow \frac{{SM}}{{MA}} = \frac{1}{2}\)

Xét tam giác \(SAB\) có \(MN\parallel AB\). Theo định lí Thales ta có:

\(\frac{{MN}}{{AB}} = \frac{{SM}}{{MA}} = \frac{1}{2} \Leftrightarrow MN = \frac{1}{2}AB = \frac{a}{2}\)

b) Ta có:

\(\begin{array}{l}BC = \left( {SBC} \right) \cap \left( {ABC{\rm{D}}} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\SK = \left( {SAD} \right) \cap \left( {SBC} \right)\\AD\parallel BC\end{array}\)

Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(SK\parallel BC\parallel A{\rm{D}}\).

-- Mod Toán 11 HỌC247