Hướng dẫn Giải bài tập Toán 11 Kết nối tri thức Chương 5 Bài 17 Hàm số liên tục môn Toán học lớp 11 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Mở đầu trang 119 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Một người lái xe từ địa điểm A đến địa điểm B trong thời gian 3 giờ. Biết quãng đường từ A đến B dài 180 km. Chứng tỏ rằng có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h.
-
Hoạt động 1 trang 119 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l} \frac{{{x^2} - 1}}{{x - 1}},x \ne 0,\\ 2,\,x = 0. \end{array} \right.\)
Tính giới hạn \(\mathop {{\rm{lim}}}\limits_{x \to 1} f\left( x \right)\) và so sánh giá trị này với f(1).
-
Luyện tập 1 trang 120 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Xét tính liên tục của hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{ - x\;,x < 0}\\{0\;,\;x = 0}\\{{x^2},x > 0}\end{array}} \right.\) tại điểm \({x_0} = 0\).
-
Hoạt động 2 trang 120 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Cho hai hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{2x\;,\;0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.\) và \(g\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x\;,0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.\) với đồ thị tương ứng như Hình 5.7
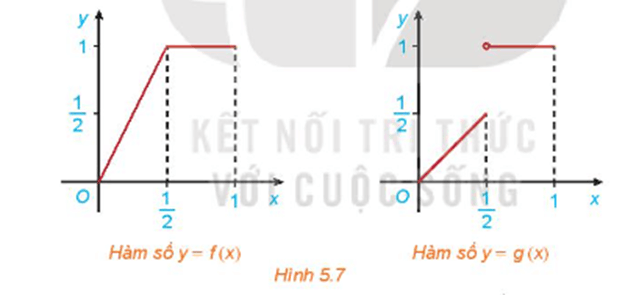
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm \(x = \frac{1}{2}\)và nhận xét về sự khác nhau giữa hai đồ thị.
-
Luyện tập 2 trang 121 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Tìm các khoảng trên đó hàm số \(f\left( x \right) = \frac{{{x^2} + 1}}{{x + 2}}\) liên tục.
-
Hoạt động 3 trang 121 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Cho hai hàm số f(x) = x2 và g(x) = – x + 1.
a) Xét tính liên tục của hai hàm số trên tại x = 1.
b) Tính \(\mathop {{\rm{lim}}}\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right]\) và so sánh L với f(1) + g(1).
-
Giải Bài 5.14 trang 122 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Cho \(f\left( x \right)\) và \(g\left( x \right)\) là các hàm số liên tục tại \(x = 1\). Biết \(f\left( 1 \right) = 2\) và \(\mathop {{\rm{lim}}}\limits_{x \to {1^ - }} \left[ {2f\left( x \right) - g\left( x \right)} \right] = 3\). Tính \(g\left( 1 \right)\).
-
Giải Bài 5.15 trang 122 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Xét tính liên tục của các hàm số sau trên tập xác định của chúng:
a) \(f\left( x \right) = \frac{x}{{{x^2} + 5x + 6}}\)
b) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{1 + {x^2}\;,\;x < 1}\\{4 - x\;\;,\;x \ge 1}\end{array}} \right.\)
-
Giải Bài 5.16 trang 122 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Tìm giá trị của tham số m để hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\sin x\;,x \ge 0}\\{ - x + m\;\;,\;x < 0}\end{array}} \right.\) liên tục trên \(\mathbb{R}\)
-
Giải Bài 5.17 trang 122 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Một bảng giá cước taxi được cho như sau:

a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển
b) Xét tính liên tục của hàm số ở câu a.
-
Bài tập 5.21 trang 86 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Cho hàm số g(x) liên tục trên \(\mathbb{R}\) trừ điểm \(x = 0\). Xét tính liên tục của hàm số \(f\left( x \right) = \frac{{g\left( x \right)}}{x}\) tại \(x = 1\)?
-
Bài tập 5.22 trang 86 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}3\;\;\;\;\;\;\;\;\;khi\;x \le 1\\ax + b\;\;khi\;1 < x < 2\\5\;\;\;\;\;\;\;\;\;khi\;x \ge 2\end{array} \right.\). Xác định a, b để hàm số liên tục trên \(\mathbb{R}\)?
-
Bài tập 5.23 trang 86 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Tìm tham số m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\;\;\;khi\;x < 1\\mx + 1\;\;khi\;x \ge 1\end{array} \right.\) liên tục trên \(\mathbb{R}\)?
-
Bài tập 5.24 trang 86 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Xét tính liên tục của các hàm số sau trên tập xác định của chúng:
a) \(f\left( x \right) = \frac{{{x^3} + x + 1}}{{{x^2} - 3x + 2}}\)
b) \(f\left( x \right) = \frac{{\cos x}}{{{x^2} + 3x - 4}}\)
-
Bài tập 5.25 trang 86 SBT Toán 11 Tập 1 Kết nối tri thức - KNTT
Chứng tỏ rằng các phương trình sau có nghiệm trong khoảng tương ứng:
a) \({x^2} = \sqrt {x + 1} \), trong khoảng \(\left( {1;2} \right)\)
b) \(\cos x = x,\) trong khoảng \(\left( {0;1} \right)\)






