Bài tập 7.10 trang 28 SBT Toán 11 Tập 2 Kết nối tri thức
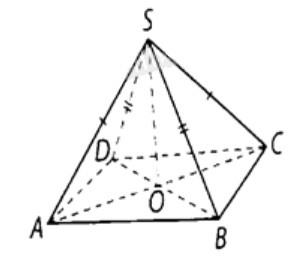
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi tâm \(O\) và \(SA = SC\), \(SB = SD\). Chứng minh rằng:
a) \(SO \bot \left( {ABCD} \right)\);
b) \(AC \bot \left( {SBD} \right)\) và \(BD \bot \left( {SAC} \right)\).
Hướng dẫn giải chi tiết Bài 7.10
a) Vì \(O\) là giao điểm của \(AC\) và \(BD\) nên \(O\) là trung điểm của \(AC\) và \(BD\) suy ra tam giác \(SAC,SBD\) cân.
Suy ra \(SO \bot AC,SO \bot BD\).
Do đó \(SO \bot \left( {ABCD} \right)\).
b) Vì \(AC \bot BD,AC \bot SO\) nên \(AC \bot \) (SBD).
Tương tự, ta được \(BD \bot \left( {SAC} \right)\).
-- Mod Toán 11 HỌC247
Nếu bạn thấy
hướng dẫn giải
Bài tập 7.10 trang 28 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT HAY thì click chia sẻ
YOMEDIA
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
