Giải bài 16 trang 38 SBT Toán 10 Cánh diều tập 2
Biểu đồ đoạn thẳng ở Hình 3 biểu diễn số lượt khách vào một cửa hàng trong ngày đầu khai trương tại một số mốc thời gian.
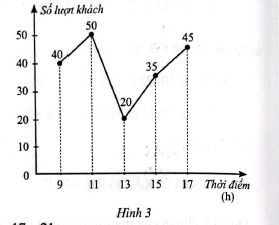
Mẫu số liệu nhận được từ biểu đồ ở Hình 3 có khoảng tứ phân vị là bao nhiêu?
A. 10 B. 15 C. 20 D. 5
Hướng dẫn giải chi tiết
Phương pháp giải
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} - {Q_1}\)
Bước 1: Sắp xếp các số liệu theo thứ tự không giảm.
Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu).
Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Lời giải chi tiết
+ Sắp xếp mẫu số liệu theo thứ tự không giảm ta được: \(20;35;40;45;50\)
+ Vì \(n = 5\) là số lẻ nên tứ phân vị thứ hai là: \({Q_2} = 40\) là tứ phân vị
+ Tứ phân vị thứ nhất là trung vị của 2 số đầu tiên của mẫu số liệu: \({Q_1} = \left( {20 + 35} \right):2 = 27,5\)
+ Tứ phân vị thứ ba là trung vị của 2 số cuối của mẫu số liệu: \({Q_3} = \left( {45 + 50} \right):2 = 47,5\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} - {Q_1} = 47,5 - 27,5 = 20\)
Chọn C.
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





