Một chậu thủy tinh nằm ngang chứa một lớp nước dày có chiết suất \({4 \over 3}\). Một tia sáng SI chiết tới mặt nước với góc tới là \({45^o}\).
a) Tính góc lệch \({D_1}\) giữa tia khúc xạ và tia tới.
b) Bỏ qua bề dày của đáy chậu. Tính góc ló của tia sáng đi ra khỏi đáy chậu và góc lệch D của tia ló này với tia tới SI.
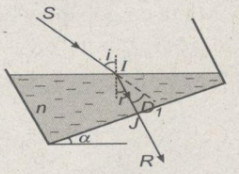
c) Giữ phương tia tới không đổi. Nghiêng đáy chậu một góc đối với mặt ngang. Hỏi giá trị của \(\alpha \) để góc lệch làm bởi tia sáng ló ra khỏi đáy chậu với tia tới SI cũng là \({D_1}\)?
Trả lời (1)
-
a) Ta có: \(\sin r = {{\sin i} \over n}\) với \(i = {45^o},n = {4 \over 3}\)
\(\eqalign{
& \sin r = 0,5302 \cr
& \Rightarrow r = {32^o} \cr} \)Suy ra: \({D_1} = i - r = {13^o}\)
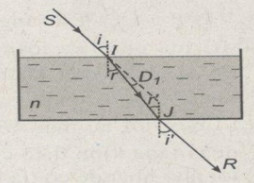
b) Góc tới tại J là r.
\(\sin i' = n\sin r = \sin i \Rightarrow i' = i\)
Do đó, tia ló JR song song với tia tới SI hay góc lệch D = 0.
c) Góc lệch giữa tia ló và tia tới bây giờ là :
\(D = {D_1} \pm {D_2}\)
Trong đó: \({D_2}\) là góc lệch tại J khi đáy chậu nghiêng một góc \(\alpha \). Ta lấy dấu (+) nếu các độ lệch \({D_1}\) và \({D_2}\) cùng chiều ; lấy dấu (-) nếu hai góc lệch này ngược chiều.
Muốn \(D = {D_1}\) ta phải có \({D_2} = 0\). Muốn vậy, ti IJ phải vuông góc với đáy chậu.
Vậy phải nghiêng chậu một góc \(\alpha = r = {32^o}\)
 bởi Ánh tuyết
bởi Ánh tuyết 05/01/2022
Like (0) Báo cáo sai phạm
05/01/2022
Like (0) Báo cáo sai phạm
Nếu bạn hỏi, bạn chỉ thu về một câu trả lời.
Nhưng khi bạn suy nghĩ trả lời, bạn sẽ thu về gấp bội!

Lưu ý: Các trường hợp cố tình spam câu trả lời hoặc bị báo xấu trên 5 lần sẽ bị khóa tài khoản
Các câu hỏi mới
-
a) tính điện dung tương đương của mạch
b) Tính điện tích và hiệu điện thế của mọi tụ
05/12/2022 | 0 Trả lời
-
Trong không khí, đặt điện tích \(q = 3.10^-8 C\) tại đỉnh của A một tam giác đề ABC. Biết cường độ điện trường do q gây ra tại B có độ lớn E=1,2*10^4 V/m và \(k=9*10^9 (N/m^2)/(C^2)\). Tính khoảng cách AB
27/12/2022 | 0 Trả lời
-
Tính suất điện động cảm ứng từ trong thanh? Nếu dùng dây có điện trở không đáng kể nối đầu thanh với một điện trở R = 0,6 thành mạch kín thì cường độ dòng điện qua điện trở bằng bao nhiêu?
12/03/2023 | 0 Trả lời
-
A. Truyền thẳng
B. Phản xạ lại theo đường truyền cũ
C. Sẽ phản xạ gương tại quang tâm O
D. Sẽ biến mất
04/04/2023 | 0 Trả lời
-
Một khung dây hình tròn có bán kính 10cm, trên dây có 500 vòng dây, khung quay đều trong từ trường đều có cảm ứng từ 0,1t. Khung quay mỗi phút được 600 vòng, lấy π2≈10. Suất điện động trong khung có độ lớn?
11/05/2023 | 0 Trả lời
-
A. 6,75.10-3 N
B. 7,8.10-3 N.
C. 0,04 N.
D. 2,5.10-3 N.
23/05/2023 | 0 Trả lời
-
Bộ nguồn được mắc với mạch ngoài là hai bóng đèn giống nhau loại 3V - 0,75W mắc song song. Cho rằng điện trở đèn không thay đổi theo nhiệt độ. Nhiệt lượng tỏa ra mỗi đèn trong 0,5 phút là
05/08/2023 | 0 Trả lời
-
Hãy giúp mình mình cần gập nhé

13/09/2023 | 0 Trả lời
-
Một vật dddh theo định luật hàm cos với tần số f=5hz.khi phá giao động là pi,giá tốc chất điểm là a=-100(m/s bình).
A. Tìm biên độ giao động
B,tìm ly độ, vận tốc chất điểm ứng với pha trên
C. Tìm giá tốc và vận tốc chất điểm khi lí độ x =12cm
15/09/2023 | 0 Trả lời
-
1 vật dao động điều hòa với tần số 2hz biên độ A=10cm
hỏi khi vật có vận tốc v=40π(cm/s) thì li độ và gia tốc bằng bao nhiêu ?
17/09/2023 | 0 Trả lời
-
Tại sao ω' = 2ω .Xin hãy giải chi tiết ạ
02/10/2023 | 0 Trả lời
-
Một vật dao động điều hòa dọc theo trục Ox, quanh điểm gốc Ox với biên độ A=24cm và chu kì T=4s. Tại thời điểm t=0 li độ là +A.
a) Viết phương trình dao động của vật
b) Tính li độ, vận tốc và gia tốc của vật tại thời điểm t=0,5s
c) Xác định thời điểm đầu tiên vật qua vị trí có li độ x=-12cm và tốc độ tối đa tại thời điểm đó
04/10/2023 | 0 Trả lời
-
A=10cm T=4s omega=pi/2
cách tính tốc độ trung bình của vật về sau khi vật đi được 9/2s kể từ vị trí ban đầu
29/10/2023 | 0 Trả lời
-
Trong giờ thực hành, một nhóm học sinh lựa chọn phương án ứng dụng sóng dừng của âm trong một ống trụ rỗng dài để đo tốc độ truyền âm trong không cach lam 12 khí như hình vẽ. Loa nối với một máy phát âm tần phát âm đủ nghe với tần số 440 Hz. Đấy từ từ pit-tông thì nhận thấy cường độ âm thay đổi. Khi chiều dài đoạn ống là l_{1}=980 mm thì âm phát ra cực đại chứng tỏ khi đó vị trí miệng ống là bụng sóng. Tiếp tục đẩy pit-tông đến vị trí chiều dài đoạn ổng là l_{2}=590 mm thì âm phát ra lại đạt cực đại.
a. Tính bước sóng và tốc độ truyền âm của sóng âm trên.
b. Hãy viết kết quả đo tốc độ truyền âm trong không khí, biết sai số tỉ đối của phép đo là 1,5%.
28/12/2023 | 0 Trả lời
-
Một electron(Điện tích -1,6.10-19C, khối lượng 9,1.10-31 kg) được bắn với vật tốc ban đầu 2.10-6 m/s vào một điện trường đều theo phương vuông góc với đường sức điện.Cường độ điện trường là 100V/m
a)Lập phương trình chuyển động,phương trình quỹ đạo của electron
b)Tính vận tốc của e khi nó chuyển động được 10-7 trong điện trường.Xác định góc lệch so với phương ban đầu lúc này
c)Một bản kim loại mang điện dương đặt vuông góc đường sức điện,cách vị trí đầu của electron đoạn 1mm.Tính tầm xa của electron khi đập ;ên bản kim loại đó.
Giải chi tiết giúp ạ18/02/2024 | 0 Trả lời
-
Câu 1: Xét một đoạn dây dẫn hình trụ có chiều dài 44cm và bán kính tiết diện 1mm đang có dòng điện 470 mA chạy qua. Biết mật độ electron trong dây dẫn bằng 8,5.1028 electron/m3. Thời gian trung bình để một electron đi hết đoạn dây trên gần đúng bằng bao nhiêu? (Đs: 40000s)
Câu 2: Một dòng điện không đổi có cường độ 1,3A chạy trong một dây dẫn bằng đồng có đường kính tiết diện 1,8mm.khối lượng riêng và khối lượng mol nguyên tử của đồng lần lượt là p= 9 tấn/m3 và A= 64 g/mol. Dạ sử mỗi nguyên tử đồng có một electron tự do.Độ lớn vận tốc của các electron tự do tạo nên dòng điện là? (Đs: 0,04 mm/s)
05/04/2024 | 0 Trả lời
-
Tính năng lượng dao động của vật.khi vật có li độ =2,5 thì vận tốc và động năng bằng bao nhiêu
12/04/2024 | 0 Trả lời
-
1 vật dao động điều hòa theo phương trình x=6cos(4pit)cm,vật tốc của vật tại thời điểm t=5s là
30/09/2024 | 0 Trả lời






