-
Câu hỏi:
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 7 và AH = 42cm. Tính độ dài các đoạn thẳng CH
- A. CH = 96
- B. CH = 49
- C. CH = 98
- D. CH = 89
Lời giải tham khảo:
Đáp án đúng: C
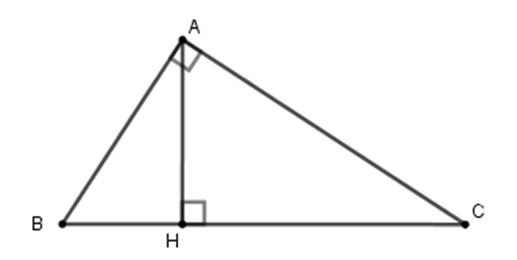
Ta có: AB : AC = 3 : 7, đặt AB = 3a; AC = 7a (a > 0)
Theo hệ thức lượng:
\(\begin{array}{*{20}{l}}
{\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Rightarrow \frac{1}{{42}} = \frac{1}{{9{a^2}}} + \frac{1}{{{{49}^2}}} \Rightarrow \frac{1}{{1764}} = \frac{{58}}{{441{a^2}}}}\\
{ \Rightarrow 441{a^2} = 102312 \Rightarrow A = 2\sqrt {58} (TM) \Rightarrow AB = 6\sqrt {58} ;AC = 14\sqrt {58} }
\end{array}\)Theo định lý Py-ta-go cho tam giác vuông AHC ta có:
\(CH = \sqrt {A{C^2} - A{H^2}} = \sqrt {{{(14\sqrt {58} )}^2} - {{42}^2}} = 98\)
Vậy CH = 98
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Tìm điều kiện xác định của \(\sqrt {5 - 3x} \)
- Hãy tìm x để \(\sqrt {\frac{{ - 2}}{{3x - 1}}} \) có nghĩa
- Rút ngọn biểu thức: A = \(\sqrt {144{a^2}} - 9a\) với a > 0
- Tính giá trị biểu thức : \(9\sqrt {{{\left( { - \frac{8}{3}} \right)}^2}} + \sqrt {{{\left( { - 0,8} \right)}^2}} \)
- Biểu thức \(\mathrm{B}=\frac{2}{\sqrt{1-3 x}}\) xác định khi
- Hãy thu gọn \(A=\sqrt{11+6 \sqrt{2}}\) ta được
- Giá trị của \(E=\sqrt{(\sqrt{3}+1)^{2}}\) là
- Biểu thức \(D=\sqrt{-x^{2}+7 x-12}\) xác định khi
- Cho tam giác ABC vuông tại A, đường cao AH. Biết rằng AB = 12cm, BH = 8cm, tính diện tích tam giác ABC.
- Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 7 và AH = 42cm.
- Cho tam giác ABC vuông tại A có đường cao AH, cho BH = 17cm, HC = 11cm. Độ dài của AH gần đúng với kết quả nào sau đây?
- Cho tam giác ABC vuông tại A có đường cao AH, cho AC = 13cm, BC = 25cm. Độ dài của CH gần đúng với kết quả nào sau đây?
- Giá trị của biểu thức \(A = \sqrt {9 - 2\sqrt {14} } + \sqrt {9 + 2\sqrt {14} } \) là?
- Kết quả rút gọn của biểu thức \(\frac{{a + \sqrt {ab} }}{{b + \sqrt {ab} }}\) (với a, b > 0) là ?
- Tính \(\sqrt {5,{5^2}{\rm{ }} - {\rm{ }}3,{5^2}{\rm{ }}} \)
- Giá trị biểu thức sau \(\sqrt {5x + 3} .\sqrt {5x - 3} \) khi \(x = \sqrt {3,6} \) là?
- Rút gọn biểu thức sau \( T = (1 + cos\alpha )(1 - cos\alpha ) - ta{n^2}\alpha + si{n^2}\alpha .ta{n^2}\alpha \)
- Cho tam giác ABC vuông tại A. Biết AB = 5, BC = 10. Giá trị của sinB và cosB lần lượt là
- Phương trình để từ đó có thể tìm được x (không phải giải phương trình này:
- Thang AB dài 6,7m tựa vào tường làm thành góc 630 với mặt đất. Hỏi chiều cao của thang đạt được so với mặt đất ?
- Tính \(a{b^2}\sqrt {\frac{3}{{{a^2}{b^4}}}} \left( {a < 0} \right)\)
- Tính \(B{\rm{ }} = {\rm{ }}\sqrt {4{\rm{ }} + {\rm{ }}\sqrt 7 } {\rm{ }} + {\rm{ }}\sqrt {4{\rm{ }} - {\rm{ }}\sqrt 7 } \)
- Giá trị của \(\frac{{\sqrt {80} }}{{\sqrt 5 }}\) bằng:
- Tính \(\frac{{\sqrt 8 }}{{\sqrt 2 }} + \frac{{\sqrt {27} }}{{\sqrt 3 }} + \frac{{\sqrt {80} }}{{\sqrt 5 }}\)
- Biểu thức \(P = \sqrt 5 \left( {\sqrt {10} - \sqrt {40} } \right)\) có giá trị bằng:
- Rút gọn biểu thức \(P = \frac{{\sqrt {16} + \sqrt {36} }}{{2\sqrt {25} }}\) ta được:
- Rút gọn biểu thức \(\sqrt {7 - 4\sqrt 3 } + \sqrt 3 \) ta được kết quả là
- Cho biết trục căn thức ở mẫu của \(\frac{2}{\sqrt{3}+1}\) ta được
- Biết: \( AB = 9cm,AC = 6,4cm;AN = 3,6cm,\widehat {AN{\rm{D}}} = {90^ \circ },\widehat {DAN} = {34^ \circ }\). Tính CN
- Để vẽ một tam giác cân có góc ở đáy là 500 mà không có thước đo góc, một học sinh vẽ một tam giác cân có cạnh bên 3cm, cạnh đáy 4cm.
- Rút gọn biểu thức sau: \( A = \frac{{3 + \sqrt 5 }}{{\sqrt 5 + 2}} + \frac{{\sqrt 5 }}{{\sqrt 5 - 1}} - \frac{{3\sqrt 5 }}{{3 + \sqrt 5 }
- Hãy tính: \( C = \frac{{\sqrt {14} + \sqrt 7 }}{{\sqrt 2 + 1}} - \sqrt 7 \)
- Tính: \( B = \sqrt {{{\left( {5 + \sqrt 3 } \right)}^2}} + \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} \)
- Giá trị x để \(A=\frac{2+5 \sqrt{x}}{\sqrt{x}+3}\) có giá trị bằng \(\frac{1}{2}\) là
- Cho tam giác ABC vuông tại A. Hãy tính \( A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\:\)
- Biết một con mèo ở trên cành cây cao 6,5m.
- Sau khi trục căn thức ở mẫu của biểu thức \( \frac{3}{{\sqrt[3]{4} + 1}}\)
- Rút gọn các biểu thức: \( \left( {15\sqrt {200} - 3\sqrt {450} + 2\sqrt {50} } \right):\sqrt {10} .\)
- So sánh hai số \(5\sqrt3\) và \(4\sqrt5\)
- Đưa thừa số \( \sqrt {144{{\left( {3 + 2a} \right)}^4}} \) ra ngoài dấu căn ta được?







