-
Câu hỏi:
Cho hình bình hành \(ABCD\) tâm \(O\). Gọi \(K,\,\,L,\,\,M,\,\,N\) tướng ứng là trung điểm các cạnh \(AB,\,\,BC,\,\,CD,\,\,DA.\) Trong các vectơ có đầu mút lấy từ các điểm \(A,\,\,B,\,\,C,\,\,D,\,\,K,\)\(L,\,\,M,\,\,O\) có bao nhiêu vectơ bằng vectơ \(\overrightarrow {AK} \) ?
- A. 2
- B. 6
- C. 4
- D. 8
Lời giải tham khảo:
Đáp án đúng: B
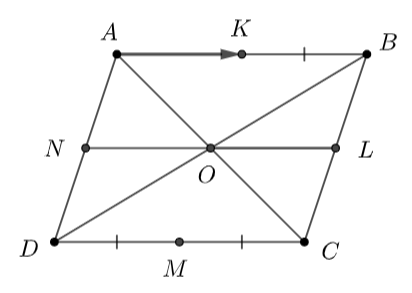
Xét hình bình hành \(ABCD\):
\( \Rightarrow \) \(AB = CD\)
mặt khác \(K\) và \(M\) lần lượt là trung điểm của \(AB\) và \(CD\)
nên \(AK = KB = CM = DM\) (1)
Ta có: \(NL\) là đường trung bình của hình bình hành \(ABCD\)
\( \Rightarrow \) \(NL\)//\(AB\)
Mặt khác \(AN\)//\(BL\)
\( \Rightarrow \) tứ giác \(ABLN\) là hình bình hành
\( \Rightarrow \) \(AB = NL\)
Ta có: \(O\) là trung điểm của \(NL\)
\(K\) là trung điểm của \(AB\)
Mặt khác \(AB = NL\)
\( \Rightarrow \) \(AK = NO = OL = AB\) (2)
Từ (1) và (2) \( \Rightarrow \) \(AK = KB = NO = OL = DM = MC\)
Mà các đường thẳng \(KB,\) \(NO,\) \(OL,\) \(DM,\) \(MC\) đều song song với \(AK\)
\( \Rightarrow \) \(\overrightarrow {AK} = \overrightarrow {KB} = \overrightarrow {NO} = \overrightarrow {OL} = \overrightarrow {DM} = \overrightarrow {MC} \)
Có 6 vectơ bằng vectơ \(\overrightarrow {AK} \)
Chọn B.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Trong các câu dưới đây, câu nào là mệnh đề?
- Trong các mệnh đề cho sau, mệnh đề nào đúng?
- Phủ định của mệnh đề “5+8=13” là mệnh đề
- Mệnh đề nào cho dưới đây đúng?
- Cho x là một phần tử của tập hợp \(X.\) Xét các mệnh đề sau:
- Cho ba tập hợp sau: \(E = \left\{ {x \in \mathbb{R}|f\left( x \right) = 0} \right\};\,\,F = \left\{ {x \in \mathbb{R}|g\left( x \right) = 0} \right\};\,\,H = \left\{ {x \in \mathbb{R}|f\left( x \right)g\left( x \right) = 0} \right\}.\)
- Cho hai tập hợp \(X = \left\{ {n \in N|n} \right.\) là bội của \(2\) và \(\left. 3 \right\},\) \(Y = \left\{ {n \in N|n} \right.\) là bội của \(\left. 6 \right\}.\) Trong các mệnh đề sau, mệnh đề nào sai?
- Trong các bất phương trình cho sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
- Trong các hệ bất phương trình dưới đây, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?
- Điểm nào sau đây thuộc miền nghiệm của bất phương trình \(2x + 5y \le 10?\)
- Điểm nào dưới đây không thuộc miền nghiệm của bất phương trình \(2x - 3y > 13?\)
- Cho bất phương trình \(x + 2y \le 3.\) Khẳng định nào sau đây là đúng?
- Cặp số nào dưới đây là nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 2}\\{x - 2y \ge 4}\\{x > 0}\end{array}\,\,?} \right.\)
- Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{ - x + y \le 2}\\{x - 2y \ge 1}\\{y \le 0}\end{array}\,\,?} \right.\)
- Tam giác \(ABC\) có \(\widehat A = {15^ \circ },\,\,\widehat B = {45^ \circ }.\) Giá trị của \(\tan C\) bằng:
- Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^ \circ }.\) Tích hoành độ và tung độ của điểm \(M\) bằng
- Trên mặt phẳng tọa độ \(Oxy,\) ta lấy điểm \(M\) thuộc nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {150^ \circ }.
- Cho góc nhọn \(\alpha \) có \(\tan \alpha = \frac{3}{4}.\) Giá trị của \(\sin \alpha .\cos \alpha \) bằng
- Cho góc nhọn \(\alpha \,\,\left( {{0^ \circ } < \alpha < {{180}^ \circ }} \right)\) thỏa mãn \(\sin \alpha + \cos \alpha = 1.\) Giá trị của \(\cot \alpha \) bằng:
- Cho góc \(\alpha \) thỏa mãn \(\sin \alpha + \cos \alpha = \sqrt 2 .\) Giá trị của \(\tan \alpha + \cot \alpha \) là:
- Số quy tròn của số gần đúng \(167,23 \pm 0,07\) là:
- Biết độ ẩm không khí tại Hà Nội là: \(51\% \pm 2\% .\) Khi đó
- Một học sinh thực hành đo chiều cao của một tòa tháp cho kết quả là 200 m. Biết chiều cao thực của tòa tháp là 201 m, sai số tương đối là:
- Cho hình bình hành \(ABCD\) tâm \(O.\) Xét các vectơ có hai điểm mút lấy từ các điểm \(A,\,\,B,\,\,C,\,\,D\) và \(O.\) Số các vectơ khác vectơ – không và cùng phương với \(\overrightarrow {AC} \) là:
- Cho đoạn thẳng \(AC\) và \(B\) là một điểm nằm giữa \(A,\,\,C.\) Trong các khẳng định sau, khẳng định nào là một khẳng định đúng?
- Cho hình bình hành \(ABCD\) tâm \(O\). Gọi \(K,\,\,L,\,\,M,\,\,N\) tướng ứng là trung điểm các cạnh \(AB,\,\,BC,\,\,CD,\,\,DA.\) Trong các vectơ có đầu mút lấy từ các điểm \(A,\,\,B,\,\,C,\,\,D,\,\,K,\)\(L,\,\,M,\,\,O\) có bao nhiêu vectơ bằng vectơ \(\overrightarrow {AK} \) ?
- Cho hình thoi \(ABCD\) có độ dài các cạnh bằng 1 và \(\widehat {DAB} = {120^ \circ }.\) Khẳng định nào sau đây là đúng?
- Một học sinh thực hành đo chiều cao của một tòa tháp cho kết quả 200 m.
- Điểm thi học kỳ môn Toán của một nhóm bạn như sau:
- Điểm thi học kỳ môn Toán của một nhóm bạn như sau: Trung vị của mẫu số liệu là:
- Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị, sao cho \(\cos \widehat {xOM} = \frac{{ - 3}}{5}.\) (H.3.4). Diện tích của tam giác \(AOM\) bằng:
- Biết trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {150^ \circ }\)
- Cho tam giác \(ABC\) đều, trọng tâm \(G,\) có độ dài các cạnh bằng 3. Độ dài vectơ \(\overrightarrow {AG} \) bằng
- Cho tam giác \(ABC\) vuông tại \(A\) và \(AB = 3,\,\,AC = 4.\) Độ dài của vectơ \(\overrightarrow {CB} + \overrightarrow {AB} \) bằng
- Cho tam giác \(ABC\) có \(AB = 2,\,\,BC = 4\) và \(\widehat {ABC} = {60^ \circ }.\) Độ dài của vectơ \(\overrightarrow {AC} - \overrightarrow {BA} \) bằng
- Cho tam giác \(ABC\) và điểm \(I\) sao cho \(\overrightarrow {IB} + 2\overrightarrow {IC} = \overrightarrow 0 .\) Khẳng định nào sau đây là một khẳng định đúng?
- Cho \(\cos \alpha = \frac{1}{4}.\) Giá trị của \(P = \frac{{\tan \alpha + 2\cot \alpha }}{{2\tan \alpha + 3\cot \alpha }}\) là:
- Tam giác \(ABC\) có \(a = 2,\,\,b = 3,\,\,c = 4.\) Bán kính đường tròn ngoại tiếp của tam giác \(ABC\) là:
- Gọi \(G\) là trọng tâm của tam giác \(ABC\) và \(M\) là trung điểm cạnh \(BC.\) Khẳng định nào sau đây là một khẳng định đúng?
- Trong mặt phẳng tọa độ \(Oxy\) cho ba điểm \(A( - 3;1),\,\,B(2; - 1),\,\,C(4;6).\) Trọng tâm \(G\) của tam giác \(ABC\) có tọa độ là:







