Câu hỏi trắc nghiệm (9 câu):
-
Câu 1:
Cho hàm số \(y=\frac{2x-m-1}{x-2}\ \ (1)\)
a.Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1) khi m = 1.
b.Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp điểm có tung độ y = 3.
c.Tìm các giá trị m ≠ 3 để hàm số (1) đồng biến trên các khoảng xác định của nó.-
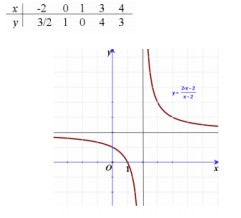
a.
+ Tập xác định: D = R \ {
 }.
}.
+ Sự biến thiên:
Đạo hàm ,
, . Hàm số nghịch biến trên mỗi khoảng
Giới hạn: , nên đường thẳng y =
, nên đường thẳng y =  là tiệm cận ngang của đồ thị (C1).
là tiệm cận ngang của đồ thị (C1). ;
; , nên đường thẳng x = 2 là tiệm cận đứng của đồ thị (C1).
, nên đường thẳng x = 2 là tiệm cận đứng của đồ thị (C1).
Bảng biến thiên:
.jpg)
* Đồ thị: Đồ thị hàm số nhận giao điểm của hai đường tiệm cận làm tâm đối xứng.
Điểm đặc biệt:
b.
Ta có:
Phương trình tiếp tuyến của (C) tại điểm M(4; 3);



c.
Ta có; tập xác định D=R\ {
 }
}
Vớihàm số đồng biến trên các khoảng


khi và chỉ khi y’ > 0,
x ≠ 2

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a.
\(y=\frac{2x-2}{x-2}\)+ Tập xác định: D = R \ {2}.
+ Sự biến thiên:
Đạo hàm \(y'=\frac{-2}{(x-2)^2}< 0,\forall x\in R\). Hàm số nghịch biến trên mỗi khoảng \((-\infty ;2),(2;+\infty )\)
Giới hạn:\(\lim_{x\rightarrow +\infty }y= \lim_{x\rightarrow -\infty }y=2\), nên đường thẳng y = 2 là tiệm cận ngang của đồ thị (C1).
\(\lim_{x\rightarrow 2^-}y=+\infty \lim_{x\rightarrow 2^-}y=-\infty\), nên đường thẳng x = 2 là tiệm cận đứng của đồ thị (C1).
Bảng biến thiên:
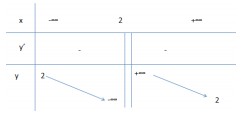
* Đồ thị: Đồ thị hàm số nhận giao điểm của hai đường tiệm cận làm tâm đối xứng.
Điểm đặc biệt:

b.
Ta có: \(y=3\Rightarrow x=4;x=4;y'(4)=-\frac{1}{2}\)
Phương trình tiếp tuyến của (C) tại điểm M(4; 3);
\(y=-\frac{1}{2}(x-4)+3\Leftrightarrow y=-\frac{1}{2}x+5\)
c.
Ta có \(y'=\frac{-3+m}{(x-2)^2}\); tập xác định D=R\ \(\begin{Bmatrix} 2 \end{Bmatrix}\)
Với \(m\neq 3\) hàm số đồng biến trên các khoảng \((-\infty ;2),(2;+\infty )\) khi và chỉ khi y’ > 0, \(\forall\)x ≠ 2
\(\Leftrightarrow m > 3\) -
-
Câu 2:
a. Cho \(sin(\pi +\alpha )=-\frac{1}{3}\) với \(\frac{\pi }{2}< \alpha < \pi\). Tính \(tan(\frac{7\pi }{2}-\alpha )\)
b. Giải bất phương trình \(8.3^{\sqrt{x}-x}+9^{\sqrt{x}-x+1}\geq 1\ \ (x\in R)\)-
a)
Ta có
Donên



b)
Điều kiện
Bất phương trình tương đương với
Đặtta có

Do vậy

Vậy tập nghiệm của bất phương trình là T = [0; 4]Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a)
Ta có \(sin(\pi +\alpha )=-\frac{1}{3}\Rightarrow sin\alpha =\frac{1}{3}\)
Do \(\frac{\pi }{2}< \alpha < \pi\) nên \(cos \alpha < 0\Rightarrow cos\alpha =-\sqrt{1-\frac{1}{9}}=-\frac{2\sqrt{2}}{3}\)
\(tan(\frac{7\pi }{2}-\alpha )=tan(3\pi +\frac{\pi }{2}-\alpha )=tan(\frac{\pi }{2}-\alpha)=cot\alpha =\frac{cos\alpha }{sin\alpha }=-2\sqrt{2}\)
b)
Điều kiện \(x\geq 0\)
Bất phương trình tương đương với \(8.3^{\sqrt{x-x}}+9.(3^{\sqrt{x-x})^2}-1\geq 0\)
Đặt \(t=3^{\sqrt{x-x}},t>0\) ta có \(9t^2+8t-1\geq 0\)
Do vậy \(3^{\sqrt{x}-x}\geq \frac{1}{9}\Leftrightarrow \sqrt{x}-x\geq -2\Leftrightarrow -x+\sqrt{x}+2\geq 0\Leftrightarrow 0\leq \sqrt{x}\leq 2\)
\(\Leftrightarrow 0\leq x\leq 4\)
Vậy tập nghiệm của bất phương trình là T = [0; 4] -
-
Câu 3:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=\sqrt{e^x+1}\) , trục hoành và hai đường thẳng: x = ln3, x = ln8.
-
Diện tích hình phẳng cần tìm là:
Đặt

Đổi cận:



Khi đó:


Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Diện tích hình phẳng cần tìm là: \(S=\int_{ln3}^{ln8}\left |\sqrt{e^x+1}-0 \right |dx=\int_{ln3}^{ln8}\sqrt{e^x+1}dx\)
Đặt \(t=\sqrt{e^x+1}\Rightarrow e^x=t^2-1\Rightarrow e^xdx=2tdt\Rightarrow dx=\frac{2t}{t^2-1}dt\)Đổi cận: \(x=ln3\Rightarrow t=2,x=ln8\Rightarrow t=3\)
Khi đó: \(S=\int_{2}^{3}\frac{2t^2}{t^2-1}dx=\int_{2}^{3}(2+\frac{1}{t-1}-\frac{1}{t+1})\)
\(=2t |_{2}^{3}+ln\left | \frac{t-1}{t+1} \right | \bigg|_{2}^{3}=2+ln\frac{3}{2}\) -
-
Câu 4:
Cho hình lăng trụ đứng ABCD A’B’C’D’ có đáy hình thoi cạnh a, \(\widehat{BAD}=60^0\) và AC' = 2a. Gọi O là giao điểm của AC và BD, E là giao điểm cả A’C và OC’. Tính thể tích khối lăng trụ ABCD A’B’C’D’ và khoảng cách từ điểm A đến mặt phẳng (EBD).
-
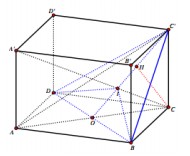
∆ABD có: AB = AD = a, nên ∆ABD đều
nên ∆ABD đều
Suy ra



Do vậy

Vẽ CHOC’ H
OC’ (1)
Ta có:(2)
Từ (1) và (2) ta có:nên d(C,(EBD))=CH
AC cắt (EBD) tại O và O là trung điểm của AC
Do vậy d(A,(EBD)) = d(C,(EBD))=CH=

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
∆ABD có: AB = AD = a, \(\widehat{BAD}=60^0\) nên ∆ABD đều
Suy ra \(AO=\frac{a\sqrt{3}}{2}\Rightarrow AC=a\sqrt{3}, CC'=a\)\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{a^2\sqrt{3}}{2}.\) Do vậy \(V_{ABCD.A'B'C'D'}=CC'.S_{ABCD}=\frac{a^3\sqrt{3}}{2}\)
Vẽ CH \(\perp\) OC’ H \(\in\) OC’ (1)
T có: \(\left.\begin{matrix} BD\perp OC\\ BD\perp CC' \end{matrix}\right\}\Rightarrow BD\perp (OCC')\Rightarrow BD\perp CH\) (2)
Từ (1) và (2) ta có: \(CH\perp (EBD)\) nên d(C,(EBD))=CH
AC cắt (EBD) tại O và O là trung điểm của AC
Do vậy d(A,(EBD)) = d(C,(EBD))=CH=\(\frac{CC'.OC}{\sqrt{CC'^2.OC^2}}=\frac{a.\frac{a\sqrt{3}}{2}}{\sqrt{a^2+\frac{3a^2}{4}}}=\frac{a\sqrt{21}}{7}\)
-
-
Câu 5:
Trong mặt phẳng tọa độ Oxy, cho tam giác nhọn ABC, gọi E, F lần lượt là hình chiếu của các đỉnh B, C lên các cạnh AC, AB. Các đường thẳng BC và EF lần lượt có phương trình BC: x - 4y - 12 = 0, EF: 8x + 49y - 6 = 0, trung điểm I của EF nằm trên đường thẳng ∆: x - 12y = 0. Tìm tọa độ các đỉnh của tam giác ABC biết BC = \(2\sqrt{17}\) và đỉnh B có hoành độ âm.
-
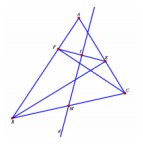
Vì I thuộc ∆ nên I (12m; m) , mà I thuộc EF nên ta có suy ra
suy ra
Gọi d là đường thẳng đi qua I và vuông góc với EF, ta có d: x - 8y -24 = 0
x - 8y -24 = 0
Đường thẳng d cắt BC tại trung điểm M của BC, do vậy M(0; -3).
Ta cónên t có phương trình:


Chọn B(-4;-4)C(4;-2)
Lấyta có
. Do vậy
và
hoặc
;
+ Với. Ta có


Suy ra(Loại vì
 )
)
. Ta có BE: 5x –
 y + 12 = 0; CF: 2x + y – 6 = 0, suy ra A(0;6) thỏa mãn
y + 12 = 0; CF: 2x + y – 6 = 0, suy ra A(0;6) thỏa mãn
Vậy A(0; 6), B(-4; -4), C(4;-2)Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
Vì I thuộc ∆ nên I (12m; m) , mà I thuộc EF nên ta có \(m=\frac{6}{145}\) suy ra \(I(\frac{72}{145};\frac{6}{145})\)
Gọi d là đường thẳng đi qua I và vuông góc với EF, ta có d: 49x - 8y -24 = 0
Đường thẳng d cắt BC tại trung điểm M của BC, do vậy M(0; -3).
T có \(BM=\sqrt{17}, B(4b+12;b), BM=\sqrt{(4b+12)^2+(b+3)^2}\)nên t có phương trình:
\((4b+12)^2+(b+3)^2=17\Leftrightarrow 17b^2+102b+136=0\Leftrightarrow \bigg \lbrack\begin{matrix} b=-2\Rightarrow B(4;-2)\\ b=-4\Rightarrow B(-4;4) \end{matrix}\)
Chọn B(-4;-4) \(\Rightarrow\) C(4;-2)
Lấy \(E(e;\frac{6-8e}{49})\) ta có \(\overline{BE}.\overline{EC}=0\). Do vậy \(E(\frac{26}{5};-\frac{2}{5})\) và \(F(-\frac{64}{5};\frac{14}{29})\) hoặc \(F(\frac{16}{5};-\frac{2}{5})\); \(E(-\frac{64}{29};\frac{14}{29})\)
+ Với \(E(\frac{16}{5};-\frac{2}{5}),F(-\frac{64}{29};\frac{14}{29})\). Ta có \(BE: x-2y-4=0, CF: 2x+5y+2=0\)
Suy ra \(A(\frac{16}{9};-\frac{10}{9})\) (Loại vì \(\overline{AB}.\overline{AC}< 0\Rightarrow cos(\overline{AB}.\overline{AC})< 0\Rightarrow \widehat{A}> 90^0\))
\(E(-\frac{64}{29};\frac{14}{29}), F(\frac{16}{5};-\frac{2}{5})\). Ta có BE: 5x – 2y + 12 = 0; CF: 2x + y – 6 = 0, suy ra A(0;6) thỏa mãn
Vậy A(0; 6), B(-4; -4), C(4;-2) -
-
Câu 6:
Trong không gian Oxyz, cho ba điểm A(-1; -2; 0), B(-5; -3; 1), C(-2; -3; 4) và đường thẳng ∆: \(\frac{x+1}{1}=\frac{y}{1}=\frac{z-2}{-1}\)
a. Chứng minh tam giác ABC đều. Tính diện tích tam giác ABC.
b. Tìm tọa độ điểm D thuộc đường thẳng ∆ sao cho thể tích tứ diện D.ABC bằng 3.-
a.
Ta có
nên tam giác ABC đều
Diện tích tam giác ABC là:


b.
Ta có


Phương trình mặt phẳng ABC A là: x – 5y – z – = 0.
= 0.
Vìnên

Vậy có hai điểm D thỏa mãn điều kiện bài toán: D -3;-2;4) hoặc D(-6;-7; 8)Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a.
T có \(AB=BC=AC=3\sqrt{2}\) nên tam giác ABC đều
Diện tích tam giác ABC là: \(S=\frac{(3\sqrt{2})^2\sqrt{3}}{4}=\frac{9\sqrt{3}}{2}\)
b.
Ta có
\(V_{D.ABC}=\frac{1}{3}d(D,(ABC)).S_{ABC}=3\Rightarrow (d(ABC))=\frac{3V}{5}=\frac{2}{\sqrt{3}}\)
\(\overline{AB}=(-4;-1;1),\overline{AC}=(-1;-1;4)\Rightarrow \left [ \overline{AB};\overline{AC} \right ]=(-3;15;3)\)
Phương trình mặt phẳng ABC A là: x – 5y – z – 9 = 0.
Vì \(D\in \Delta\) nên \(D(-1+t;t;2-t)\)
\(d(D;(ABC))=\frac{2}{\sqrt{3}}\Leftrightarrow \frac{\left | -1+t-5t-2+t-9\right |}{3\sqrt{3}}=\frac{2}{\sqrt{3}}\)
\(\Leftrightarrow \left | 3t+12 \right |=6\Leftrightarrow \bigg \lbrack\begin{matrix} t=-2\\ t=-6 \end{matrix}\)
Vậy có hai điểm D thỏa mãn điều kiện bài toán: D -3;-2;4) hoặc D(-6;-7; 8) -
-
Câu 7:
a. Giải phương trình \(\sqrt{3x+2}+\sqrt{2x+1}=x+1\ \ (x\in R)\)
b. Từ tập E = {1; 2; 3; 4; 5}, lập các số tự nhiên có ba chữ số. Lấy ngẫu nhiên hai số trong các số vừa lập. Tính xác suất để trong hai số được lấy ra có ít nhất một số có đúng hai chữ số phân biệt.-
a.
Điều kiện:

Với điều kiện đó, ta có:


(thỏa mãn điều kiện)
b.
Từ tập hợp E=ta có thể lập được

 số có chữ số. Chọn 2 số từ 125 số ở trên có
số có chữ số. Chọn 2 số từ 125 số ở trên có cách.
Gọi A là biến cố: “Hai số được chọn có ít nhất một số có đúng hai chữ số phân biệt”
Trong 125 số trên có số có ba chữ số trong đó có đúng hai chữ số phân biệt.
số có ba chữ số trong đó có đúng hai chữ số phân biệt.
Do vậy
Vậy xác suất cần tìm là:Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a.
Điều kiện: \(x\geq \frac{1}{2}\)
Với điều kiện đó, ta có: \(\sqrt{3x+2}+\sqrt{2x+1}=x+1\)
\(\Leftrightarrow \sqrt{3x+2}+\sqrt{2x+1}=(\sqrt{3x+2}+\sqrt{2x+1})(\sqrt{3x+2}-\sqrt{2x+1})\)
\(\Leftrightarrow (\sqrt{3x+2}+\sqrt{2x+1})(\sqrt{3x+2}-\sqrt{2x+1})=0\)
\(\Leftrightarrow (\sqrt{3x+2}-\sqrt{2x+1})=1 \ (do \ \ \sqrt{3x+2}+\sqrt{2x+1}> 0)\)
\(\Leftrightarrow \sqrt{3x+2}=\sqrt{2x+1}+1\)
\(\Leftrightarrow 3x+2 =2x+1+1+2\sqrt{2x+1}\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq 0\\ x^2-8x-4=0 \end{matrix}\right.\)
\(\Leftrightarrow x=4+2\sqrt{5}\) (thỏa mãn điều kiện)
Vậy phương trình có nghiệm là: \(x=4+2\sqrt{5}\)
b.
Từ tập hợp E= \(\begin{Bmatrix} 1;2;3;4;5 \end{Bmatrix}\) ta có thể lập được \(5^3=125\) số có chữ số. Chọn 2 số từ 125 số ở trên có \(C_{125}^{2}\) cách.
Gọi A là biến cố: “Hai số được chọn có ít nhất một số có đúng hai chữ số phân biệt”
Trong 125 số trên có \(C_{125}^{2}.6=60\) số có ba chữ số trong đó có đúng hai chữ số phân biệt. Do vậy \(n(\Omega _A)=60.65+C_{60}^{2}\)
Vậy xác suất cần tìm là: \(P=\frac{60.65+C_{60}^{2}}{C_{125}^{2}}=\frac{567}{775}\approx 0,73\) -
-
Câu 8:
Tìm số phức z biết. \((z+3-i)^2-6(z+3-i)+13=0\)
-
Đặt t = z +
 – i, phương trình trở thành: t2 -
– i, phương trình trở thành: t2 -  t +
t +  = 0
= 0
Ta có:

có hai căn bậc hai là ±
Phương trình trên có hai nghiệm phức là t = 3 - i hoặc t =
i hoặc t =  + 2i
+ 2i
Do vậy z + 3 – i = – 2i hoặc z + 3 – i = 3 + 2i
– 2i hoặc z + 3 – i = 3 + 2i
Vậy z = - i hoặc z = 3iCác em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Đặt t = z + 3 – i, phương trình trở thành: t2 - 6t 13 = 0
Ta có: \(\Delta '=-4=4i^2,\Delta '\) có h i căn bậc hai là ±
Phương trình trên có hai nghiệm phức là t = 3 - 2i hoặc t = 3 + 2i
Do vậy z + 3 – i = 3 – 2i hoặc z + 3 – i = 3 + 2i
Vậy z = - i hoặc z = 3i -
-
Câu 9:
Cho a, b, c ≥ 1 là các số thực dương thỏa mãn a + b + c = 6. Tìm giá trị lớn nhất của:
\(P=(a^2+2)(b^2+2)(c^2+2)\)-
Không mất tổng quát có thể giả sử
. Suy ra
. Suy ra
Ta chứng minh bất đẳng thức
Thật vậy, bất đẳng thức tương đương với



Bất đẳng thức cuối cùng đúng bởi vì
Đặtta có:

Vìnên ta có

Hơn nữanên ta có
Ta cần tìm giá trị lớn nhất của
trên
và
Nhưng f(2) = 216 nên f(x) đạt GTLN bằng 216, dấu bằng xảy ra khi và chỉ khi x = 2.
Vậy ta có, hay P đạt GTLN bằng 216, dấu bằng xảy ra khi và chỉ khi a =b = c =

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Không mất tổng quát có thể giả sử \(a\geq b\geq c\). Suy ra \(6 = a +b + c \geq c+c+c\) . Suy ra \(c\geq 2;a+b\geq 4\)
Ta chứng minh bất đẳng thức \((a^2+2)(b^2+2)\leq (\left ( \frac{a+b}{2} \right )^2+2)^2\)
Thật vậy, bất đẳng thức tương đương với
\(a^2+b^2+2a^2+2b^2\leq \frac{(a+b)^4}{16}+(a+b)^2\Leftrightarrow 16(a-b)^2\leq (a+b)^4-16a^2b^2\)
\(\Leftrightarrow 16(a-b)^2\leq (a^2-b^2)^2+4ab(a-b)^2\)
\(\Leftrightarrow 16(a-b)^2\leq (a-b)^2\left [ (a+b)^2+4ab \right ]\)
Bất đẳng thức cuối cùng đúng bởi vì \((a+b)^2\geq 4^2=16\)
Đặt \(x=\frac{a+b}{2}\) ta có:
\((a^2+2)(b^2+2)(c^2+2)\leq (x^2+2)^2(c^2+2)=(x^2+2)^2((6-2x)^2+2)\)
Vì \(c\geq 1\) nên ta có \(2x+c=6\Rightarrow x\leq \frac{5}{2}\)
Hơn nữa \(2x=a+b\geq 4\) nên ta có \(x\in \left [ 2;\frac{5}{4} \right ]\)
Ta cần tìm giá trị lớn nhất của
\(\small f(x)=(x^2+2)^2\left [ (6-2x)^2+2 \right ]=4x^6-24x^5+54x^4-96x^3+168x^2-96x+152\) trên \(\small \left [ 2;\frac{5}{2} \right ]\)
\(\small f'(x)=12(x^2+2)(x-2)(x^2-3x+1)\) và \(\small f'(x)< 0,\forall x\in (2;\frac{5}{2})\)
Nhưng f(2) = 216 nên f(x) đạt GTLN bằng 216, dấu bằng xảy ra khi và chỉ khi x = 2.
Vậy ta có \(\small (a^2+2)(b^2+2)(c^2+2)\leq 216\), hay P đạt GTLN bằng 216, dấu bằng xảy ra khi và chỉ khi a =b = c = 2. -





