Giải câu hỏi 2 trang 82 SGK Vật Lý 10 Kết nối tri thức
Một quyển sách đặt trên mặt bàn nghiêng và được thả cho trượt xuống. Cho biết góc nghiêng \(\alpha = {30^ \circ }\) so với phương ngang và hệ số ma sát giữa quyển sách và mặt bàn là \(\mu = 0,3\). Lấy g = 9,8 m/s2 . Tính gia tốc của quyển sách và quãng đường đi được của nó sau 2 s.
Hướng dẫn giải chi tiết câu hỏi 2 trang 82
Hướng dẫn giải
Các bước giải bài toán phần động lực học:
+ Bước 1: Phân tích lực tác dụng lên vật
+ Bước 2: Chọn hệ quy chiếu
+ Bước 3: Viết phương trình theo định luật 2 Newton: \(\sum {\overrightarrow F } = m.\overrightarrow a \)
+ Bước 4: Chiếu phương trình định luật 2 Newton lên trục Ox và Oy => Đại lượng cần tính
Lời giải chi tiết
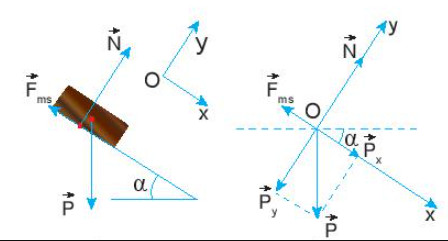
Quyển sách (coi là chất điểm) chịu tác dụng của ba lực: lực ma sát \(\overrightarrow {{F_{ms}}} \), trọng lực \(\overrightarrow P \), phản lực \(\overrightarrow N \)
Theo định luật 2 Newton, ta có:
\(\overrightarrow {{F_{ms}}} + \overrightarrow P + \overrightarrow N = m.\overrightarrow a \) (1)
Chiếu (1) lên Ox, ta có:
\({P_x} - {F_{ms}} = ma\)
\( \Leftrightarrow mg\sin \alpha - \mu N = ma\) (2)
Chiếu (1) lên Oy, ta có:
\(\begin{array}{l}N - {P_y} = 0\\ \Leftrightarrow N - mg\cos \alpha = 0\\ \Leftrightarrow N = mg\cos \alpha \end{array}\)
Thay \(N = mg\cos \alpha \) vào (2), ta có:
\(\begin{array}{l}mg\sin \alpha - \mu mg\cos \alpha = ma\\ \Leftrightarrow g\sin \alpha - \mu g\cos \alpha = a\\ \Leftrightarrow a = 9,8.\sin {30^ \circ } - 0,3.9,8.\cos {30^ \circ }\\ \Leftrightarrow a \approx 2,35(m/{s^2})\end{array}\)
Quãng đường vật đi được sau 2 s là:
\(S = \frac{1}{2}a{t^2} = \frac{1}{2}.2,{35.2^2} = 4,7(m)\)
-- Mod Vật Lý 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





