Đề thi thử tốt nghiệp THPT môn Toán năm 2022-2023 Trường THPT Herman-Gmeiner có đáp án có cấu trúc bám sát với đề minh họa, nhằm giúp học sinh làm quen với các dạng câu hỏi và củng cố kĩ năng làm bài. Đề thi gồm 40 câu trắc nghiệm từ câu 41-80 kèm theo đáp án chi tiết. Hi vọng tài liệu này sẽ hữu ích cho quá trình ôn tập và chuẩn bị cho kì thi THPT sắp tới. Chúc các em thi tốt!
Số báo danh:…………………………………………………. Mỗi câu trả lời đúng được 0,2 điểm. |
1. Đề thi
Câu 1. Trong không gian \(Oxyz\) , cho mặt phẳng \((P):3x+y-2z+1=0\) . Vectơ nào sau đây là một vectơ pháp tuyến của \((P)\) ?
A. \({{\vec{n}}_{1}}=\left( 1\,;\,-2\,;\,1 \right)\) .
B. \({{\vec{n}}_{2}}=\left( 3\,;\,-2\,;\,1 \right)\) .
C. \({{\vec{n}}_{3}}=\left( -2\,;\,1\,;\,3 \right)\) .
D. \({{\vec{n}}_{4}}=\left( 3\,;\,1\,;\,-2 \right)\) .
Câu 2. Số cách xếp 4 người thành một hàng ngang là
A. \(A_{4}^{2}\) .
B. \({{4}^{4}}\) .
C. \(C_{4}^{4}\) .
D. \(4!\) .
Câu 3. Cho hàm số \(y=f(x)\) có đồ thị là đường cong như hình bên dưới.
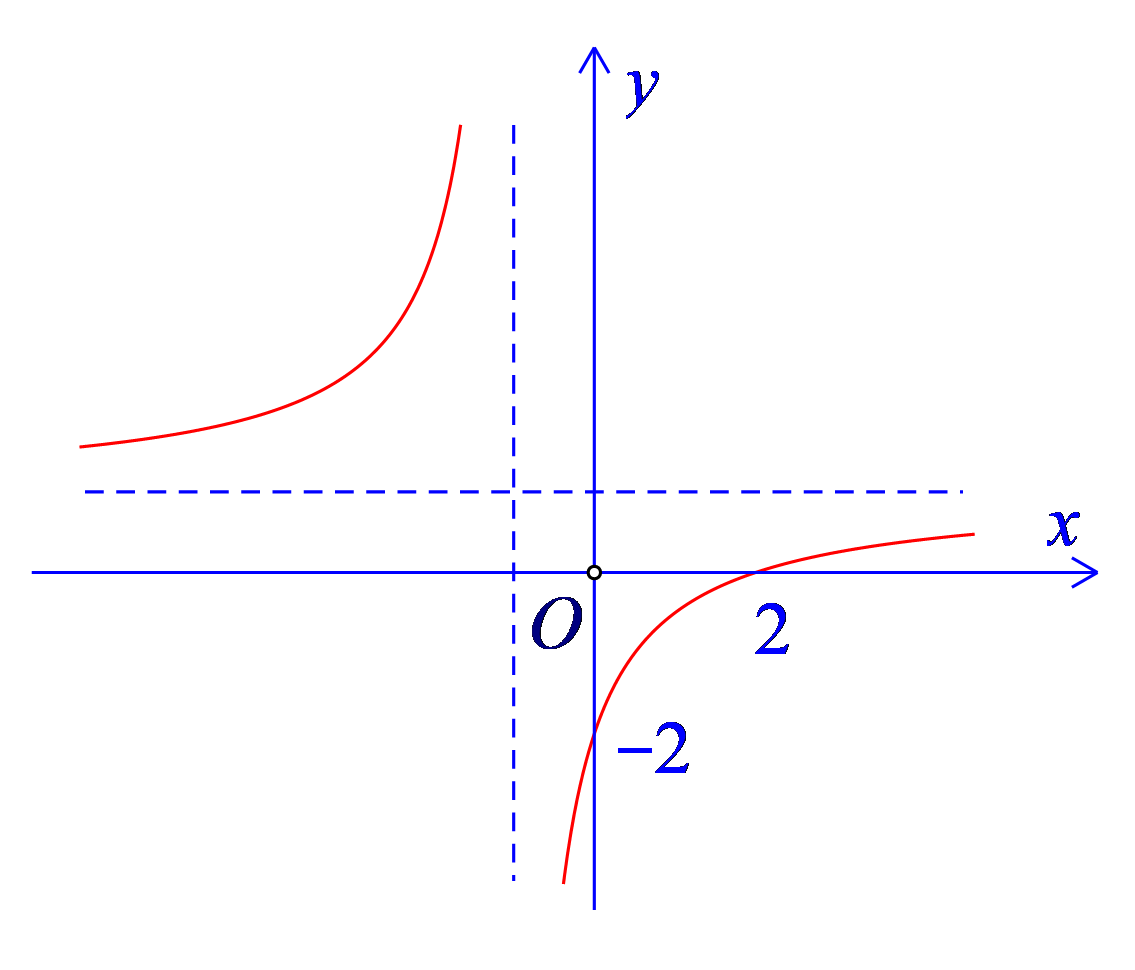
Đồ thị hàm số đã cho cắt trục hoành tại điểm nào sau đây?
A. \((2;0)\).
B. \((0;2)\).
C. \((-2;0)\).
D. \((0;-2)\).
Câu 4. Tập xác định của hàm số \(y={{x}^{\sqrt{5}}}\) là
A. \(\left( 0\,;\,+\infty \right)\).
B. \(\left[ 0\,;\,+\infty \right)\).
C. \(\left( -\infty \,;\,0 \right)\).
D. \(\left( -\infty \,;\,+\infty \right)\).
Câu 5. Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(a\) là số thực dương. Khẳng định nào dưới đây đúng?
A. \(\int\limits_{-a}^{a}{f\left( x \right)\text{d}x}=0\).
B. \(\int\limits_{-a}^{0}{f\left( x \right)\text{d}x}=0\).
C. \(\int\limits_{0}^{a}{f\left( x \right)\text{d}x}=0\).
D. \(\int\limits_{a}^{a}{f\left( x \right)\text{d}x}=0\).
Câu 6. Thể tích của khối cầu có bán kính \(R\) là
A. \(\frac{4}{3}\pi {{R}^{3}}\).
B. \(\frac{1}{3}\pi {{R}^{3}}\).
C. \(4\pi {{R}^{3}}\).
D. \(\frac{4}{3}\pi {{R}^{2}}\).
Câu 7. Môđun của số phức \(z=4-3i\) bằng
A. \(5\) .
B. \(\sqrt{7}\).
C. \(25\).
D. \(7\).
Câu 8. Giá trị của \(\int\limits_{2}^{5}{\frac{1}{x}\text{d}x}\) bằng
A. \(\ln \frac{5}{2}\).
B. \(\ln \frac{2}{5}\).
C. \(\frac{1}{3}\ln 3\).
D. \(3\ln 3\).
Câu 9. Trong không gian \(Oxyz\), đường thẳng đi qua điểm \(M\left( 3;\,-1;\,2 \right)\) và có vectơ chỉ phương \(\overrightarrow{u}=\left( 4;\,5;\,-7 \right)\) có phương trình là
A. \(\frac{x+3}{4}=\frac{y-1}{5}=\frac{z+2}{-7}\).
B. \(\frac{x+4}{3}=\frac{y+5}{-1}=\frac{z-7}{2}\).
C. \(\frac{x-4}{3}=\frac{y-5}{-1}=\frac{z+7}{2}\).
D. \(\frac{x-3}{4}=\frac{y+1}{5}=\frac{z-2}{-7}\).
Câu 10. Trong không gian \(Oxyz\), cho hai véctơ \(\vec{a}=\left( 2\,;\,3\,;\,2 \right)\) và \(\vec{b}=\left( 1\,;\,1\,;\,-1 \right)\). Véctơ \(\vec{a}-\vec{b}\) có toạ độ là
A. \(\left( -1\,;\,-2\,;\,3 \right)\).
B. \(\left( 3\,;\,5\,;\,1 \right)\).
C. \(\left( 3\,;\,4\,;\,1 \right)\).
D. \(\left( 1\,;\,2\,;\,3 \right)\).
Câu 11. Cho khối lăng trụ có diện tích đáy bằng \(B\) và chiều cao bằng \(h\). Thể tích \(V\) của khối lăng trụ đã cho được tính theo công thức nào dưới đây?
A. \(V=\frac{1}{2}Bh\).
B. \(V=Bh\).
C. \(V=3Bh\).
D. \(V=\frac{1}{3}Bh\).
Câu 12. Điểm \(M\) trong hình bên dưới biểu diễn số phức nào sau đây?
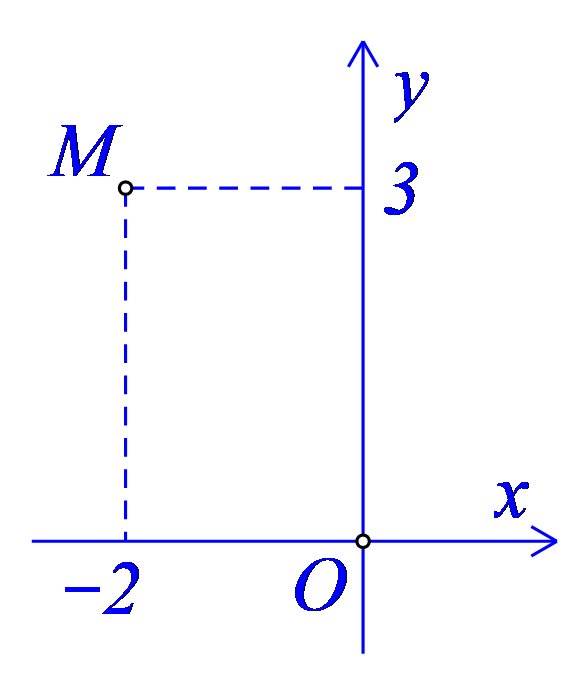
A. \({{z}_{3}}=-2+3i\).
B. \({{z}_{2}}=2-3i\).
C. \({{z}_{1}}=3+2i\).
D. \({{z}_{4}}=3-2i\).
Câu 13. Thể tích của khối trụ có chiều cao \(h=2\) và bán kính đáy \(r=3\) là
A. \(6\pi \).
B. \(9\pi \).
C. \(15\pi \) \(\).
D. \(18\pi \).
Câu 14. Hàm số nào sau đây có đồ thị là đường cong như hình bên dưới?
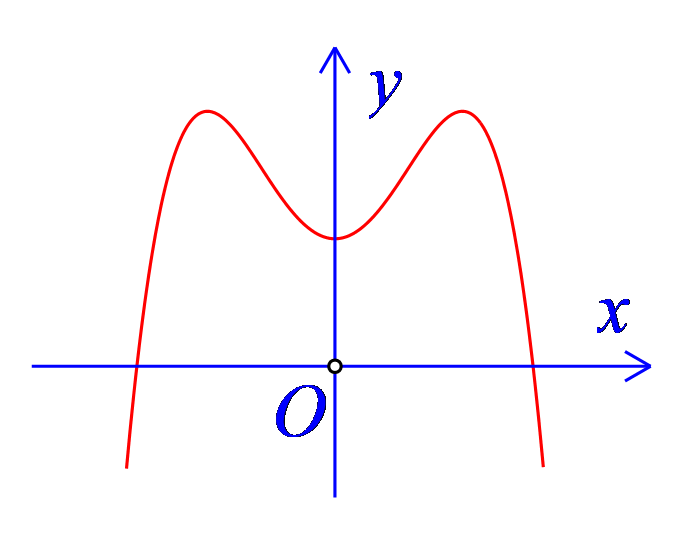
A. \(y={{x}^{4}}-2{{x}^{2}}+1\).
B. \(y=-{{x}^{4}}+2{{x}^{2}}+1\).
C. \(y=-{{x}^{3}}+3{{x}^{2}}+1\).
D. \(y={{x}^{3}}-3{{x}^{2}}+1\).
Câu 15. Trong không gian \(Oxyz\) , điểm nào dưới đây thuộc đường thẳng \(d:\frac{x-1}{2}=\frac{y}{1}=\frac{z+1}{2}?\)
A. \(N\left( -1;0;1 \right)\).
B. \(Q\left( -2;-1;-2 \right)\).
C. \(M\left( 2;1;2 \right)\).
D. \(P\left( 1;0;-1 \right)\).
Câu 16. Nghiệm của phương trình \({{3}^{x}}=7\) là
A. \(x={{3}^{7}}\).
B. \(x={{\log }_{7}}3\).
C. \(x=\frac{7}{3}\).
D. \(x={{\log }_{3}}7\).
Câu 17. Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(k\) là một số thực khác 0. Khẳng định nào dưới đây đúng?
A. \(\int{kf\left( x \right)\text{d}x=k\int{f\left( x \right)\text{d}x}}\) .
B. \(\int{kf\left( x \right)\text{d}x=k+\int{f\left( x \right)\text{d}x}}\) .
C. \(\int{kf\left( x \right)\text{d}x=\int{k\,\text{d}x}.\int{f\left( x \right)\text{d}x}}\) .
D. \(\int{kf\left( x \right)\text{d}x=\frac{1}{k}\int{f\left( x \right)\text{d}x}}\) .
...
2. Đáp án
BẢNG ĐÁP ÁN
|
1.D |
2.D |
3.A |
4.A |
5.D |
6.A |
7.A |
8.A |
9.D |
10.D |
|
11.B |
12.A |
13.D |
14.B |
15.D |
16.D |
17.A |
18.D |
19.C |
20.A |
|
21.A |
22.A |
23.B |
24.A |
25.B |
26.B |
27.A |
28.C |
29.B |
30.D |
|
31.A |
32.C |
33.C |
34.A |
35.C |
36.D |
37.A |
38.B |
39.A |
40.A |
|
41.D |
42.A |
43.B |
44.A |
45.D |
46.D |
47.A |
48.B |
49.A |
50.C |
LỜI GIẢI CHI TIẾT
Câu 1. [ Mức độ 1] Trong không gian \(Oxyz\) , cho mặt phẳng \((P):3x+y-2z+1=0\) . Vectơ nào sau đây là một vectơ pháp tuyến của \((P)\) ?
A. \({{\vec{n}}_{1}}=\left( 1\,;\,-2\,;\,1 \right)\) . B. \({{\vec{n}}_{2}}=\left( 3\,;\,-2\,;\,1 \right)\) . C. \({{\vec{n}}_{3}}=\left( -2\,;\,1\,;\,3 \right)\) . D. \({{\vec{n}}_{4}}=\left( 3\,;\,1\,;\,-2 \right)\) .
Lời giải
Vectơ pháp tuyến của \((P)\) là \({{\vec{n}}_{4}}=\left( 3\,;\,1\,;\,-2 \right)\) .
Câu 2. [ Mức độ 1] Số cách xếp 4 người thành một hàng ngang là
A. \(A_{4}^{2}\) . B. \({{4}^{4}}\) . C. \(C_{4}^{4}\) . D. \(4!\) .
Lời giải
Số cách xếp 4 người thành một hàng ngang là số hoán vị 4 phần tử:\({{P}_{4}}=4!\) .
Câu 3. [ Mức độ 1] Cho hàm số \(y=f(x)\) có đồ thị là đường cong như hình bên dưới.

Đồ thị hàm số đã cho cắt trục hoành tại điểm nào sau đây?
A. \((2;0)\). B. \((0;2)\). C. \((-2;0)\). D. \((0;-2)\).
Lời giải
Quan sát hình vẽ ta thấy đồ thị hàm số đã cho cắt trục hoành tại điểm \((2;0)\) .
Câu 4. [ Mức độ 1] Tập xác định của hàm số \(y={{x}^{\sqrt{5}}}\) là
A. \(\left( 0\,;\,+\infty \right)\). B. \(\left[ 0\,;\,+\infty \right)\). C. \(\left( -\infty \,;\,0 \right)\). D. \(\left( -\infty \,;\,+\infty \right)\).
Lời giải
Hàm số \(y={{x}^{\sqrt{5}}}\) là hàm số lũy thừa với số mũ là \(\alpha =\sqrt{5}\notin \mathbb{Z}\) nên điều kiện xác định là \(x>0\).
Vậy tập xác định của hàm số đã cho là \(\left( 0\,;\,+\infty \right)\).
Câu 5. [ Mức độ 1] Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(a\) là số thực dương. Khẳng định nào dưới đây đúng?
A. \(\int\limits_{-a}^{a}{f\left( x \right)\text{d}x}=0\). B. \(\int\limits_{-a}^{0}{f\left( x \right)\text{d}x}=0\). C. \(\int\limits_{0}^{a}{f\left( x \right)\text{d}x}=0\). D. \(\int\limits_{a}^{a}{f\left( x \right)\text{d}x}=0\).
Lời giải
Theo tính chất tích phân ta có \(\int\limits_{a}^{a}{f\left( x \right)\text{d}x}=0\).
Giải thích: Gọi \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\).
Ta có: \(\int\limits_{a}^{a}{f\left( x \right)\text{d}x}=\left. F\left( x \right) \right|_{a}^{a}=F\left( a \right)-F\left( a \right)=0\).
Câu 6. [ Mức độ 1] Thể tích của khối cầu có bán kính \(R\) là
A. \(\frac{4}{3}\pi {{R}^{3}}\). B. \(\frac{1}{3}\pi {{R}^{3}}\). C. \(4\pi {{R}^{3}}\). D. \(\frac{4}{3}\pi {{R}^{2}}\).
Lời giải
Theo lý thuyết công thức tính thể tích khối cầu có bán kính \(R\) là \(\frac{4}{3}\pi {{R}^{3}}\).
Câu 7. Môđun của số phức \(z=4-3i\) bằng
A. \(5\) . B. \(\sqrt{7}\). C. \(25\). D. \(7\).
Lời giải
Ta có \(z=4-3i\) \(\Rightarrow \left| z \right|=\sqrt{{{4}^{2}}+{{\left( -3 \right)}^{2}}}=5\) .
Câu 8. Giá trị của \(\int\limits_{2}^{5}{\frac{1}{x}\text{d}x}\) bằng
A. \(\ln \frac{5}{2}\). B. \(\ln \frac{2}{5}\). C. \(\frac{1}{3}\ln 3\). D. \(3\ln 3\).
Lời giải
Ta có \(\int\limits_{2}^{5}{\frac{1}{x}dx}=\left. \ln \left| x \right| \right|_{2}^{5}=\ln 5-\ln 2=\ln \frac{5}{2}\).
Câu 9. Trong không gian \(Oxyz\), đường thẳng đi qua điểm \(M\left( 3;\,-1;\,2 \right)\) và có vectơ chỉ phương \(\overrightarrow{u}=\left( 4;\,5;\,-7 \right)\) có phương trình là
A. \(\frac{x+3}{4}=\frac{y-1}{5}=\frac{z+2}{-7}\). B. \(\frac{x+4}{3}=\frac{y+5}{-1}=\frac{z-7}{2}\).
C. \(\frac{x-4}{3}=\frac{y-5}{-1}=\frac{z+7}{2}\). D. \(\frac{x-3}{4}=\frac{y+1}{5}=\frac{z-2}{-7}\).
Lời giải
Đường thẳng đi qua điểm \(M\left( 3;\,-1;\,2 \right)\) và có vectơ chỉ phương \(\overrightarrow{u}=\left( 4;\,5;\,-7 \right)\) có phương trình chính tắc là: \(\frac{x-3}{4}=\frac{y+1}{5}=\frac{z-2}{-7}\).
Câu 10. Trong không gian \(Oxyz\), cho hai véctơ \(\vec{a}=\left( 2\,;\,3\,;\,2 \right)\) và \(\vec{b}=\left( 1\,;\,1\,;\,-1 \right)\). Véctơ \(\vec{a}-\vec{b}\) có toạ độ là
A. \(\left( -1\,;\,-2\,;\,3 \right)\). B. \(\left( 3\,;\,5\,;\,1 \right)\). C. \(\left( 3\,;\,4\,;\,1 \right)\). D. \(\left( 1\,;\,2\,;\,3 \right)\).
Lời giải
Ta có: \(\vec{a}-\vec{b}=\left( 2-1\,;\,3-1\,;\,2+1 \right)\Rightarrow \vec{a}-\vec{b}=\left( 1\,;\,2\,;\,3 \right)\).
...
---(Để xem đầy đủ nội dung đề thi và đáp án chi tiết, các em vui lòng xem online hoặc đăng nhập để tải về máy)---
Trên đây là một phần trích đoạn nội dung Đề thi thử tốt nghiệp THPT môn Toán năm 2022-2023 Trường THPT Herman-Gmeiner có đáp án. Để xem thêm nhiều tài liệu tham khảo hữu ích khác các em chọn chức năng xem online hoặc đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.
Chúc các em học tập tốt!







