Luyện tập 1 trang 65 SGK Toán 8 Kết nối tri thức tập 1
Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH ⊥ DC (H ∈ DC)(H.3.44). Chứng minh rằng H là trung điểm của DC.
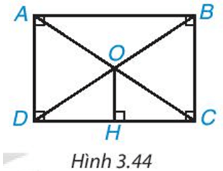
Hướng dẫn giải chi tiết Luyện tập 1
Vì ABCD là hình chữ nhật có hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Suy ra OA = OB = OC = OD.
Xét tam giác OCD cân tại O (vì OC = OD) có OH là đường cao nên OH cũng là đường trung tuyến.
Do đó CH = DH.
Vậy H là trung điểm của DC.
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Hoạt động 1 trang 64 SGK Toán 11 Kết nối tri thức tập 1 - KNTT
Hoạt động 2 trang 64 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Hoạt động 3 trang 65 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Luyện tập 2 trang 66 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Vận dụng trang 66 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Bài 3.25 trang 66 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Bài 3.26 trang 66 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Bài 3.27 trang 66 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Bài 3.28 trang 66 SGK Toán 8 Kết nối tri thức tập 1 - KNTT
Bài tập 3.20 trang 39 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.21 trang 39 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT
Bài tập 3.22 trang 39 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT





