Bài tập 3.20 trang 39 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT

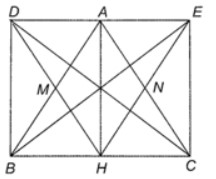
a) • Tứ giác AHBD có M là trung điểm của AB và HD nên là hình bình hành.

Do AH là đường cao của ∆ABC nên AH ⊥ BC, suy ra $\widehat{AHB}=90°$

Hình bình hành AHBD có $\widehat{AHB}=90°$ nên AHBD là hình chữ nhật.

• Tương tự, tứ giác AHCE có N là trung điểm của AC và HE nên là hình bình hành.

Lại có $\widehat{AHC}=90°$ nên AHCE là hình chữ nhật.

• Do AHBD, AHCE là các hình chữ nhật (chứng minh trên)

Suy ra $\widehat{ADB}=\widehat{DBH}=\widehat{HCE}=\widehat{AEC}=90°$

Tứ giác BCED có $\widehat{ADB}=\widehat{DBH}=\widehat{HCE}=\widehat{AEC}=90°$ là các góc ở đỉnh nên BCED là hình chữ nhật.

b) Vì ADBH, AECH là các hình chữ nhật nên AD = BH, AE = HC, AD // BC, AE // BC

Mà ∆ABC cân tại A có AH là đường cao nên đồng thời là đường trung tuyến, do đó H là trung điểm của BC, suy ra BH = HC.

Từ đó, AD = BH = HC = AE

Tứ giác ADHC có: AD // HC, AD = HC nên ADHC là hình bình hành.

Tứ giác ABHE có: AE // BH, AE = BH nên ABHE là hình bình hành

Vì ADHC là hình bình hành nên CD cắt AH tại trung điểm của AH.

Vì AEHB là hình bình hành nên BE cắt AH tại trung điểm của AH.

Vậy giao điểm của BE và CD là trung điểm của AH.

c) Do AHBD, AHCE là các hình chữ nhật nên AB = DH, AC = HE (hai đường chéo bằng nhau).

Mà AB = AC (do ∆ABC cân tại A) nên DH = HE.

Do BCED là hình chữ nhật (chứng minh câu a) nên CD = BE (hai đường chéo bằng nhau).

-- Mod Toán 8 HỌC247