Phần hướng dẫn giải bài tập Toán 8 Cánh Diều Chương 8 Bài 8 Trường hợp đồng dạng thứ ba của tam giác sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng, giải bài tập từ SGK Toán 8 Tập 2 Cánh Diều.
-
Hoạt động 1 trang 83 SGK Toán 8 Tập 2 Cánh diều - CD
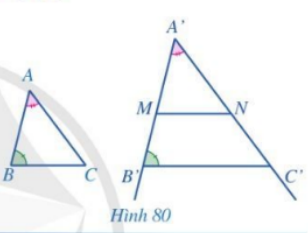
Cho hai tam giác ABC, A’B’C’ sao cho \(\widehat {A'} = \widehat A,\,\,\widehat {B'} = \widehat B\) và \(A'B' \ne AB\) (Hình 80). Trên tia A’B’ lấy điểm M khác B thỏa mãn \(A'M = AB\). Qua M kẻ đường thẳng song song với B’C’ cắt tia A’C’ tại N. Chứng minh \(\Delta A'MN = \Delta ABC\). Từ đó suy ra \(\Delta A'B'C' \backsim \Delta ABC\)?
-
Luyện tập 1 trang 83 SGK Toán 8 Tập 2 Cánh diều - CD
Cho hai tam giác ABC và MNP thỏa mãn \(\widehat A = 50^\circ ,\,\,\widehat B = 60^\circ ,\,\,\widehat N = 60^\circ ,\,\,\widehat P = 70^\circ \). Chứng minh \(\Delta ABC \backsim \Delta MNP\)?
-
Hoạt động 2 trang 84 SGK Toán 8 Tập 2 Cánh diều - CD
Cho hai tam giác ABC và A’B’C’ có \(\widehat {A'} = \widehat A = 90^\circ ,\,\,\widehat {B'} = \widehat B\) (Hình 84). Chứng minh \(\Delta A'B'C' \backsim \Delta ABC\)?

-
Luyện tập 2 trang 84 SGK Toán 8 Tập 2 Cánh diều - CD
Cho tam giác nhọn ABC có hai đường cao AD, BE cắt nhau tại H. Chứng minh \(HA.HD = HB.HE\)?
-
Bài 1 trang 85 SGK Toán 8 Tập 2 Cánh diều - CD
Cho Hình 86.
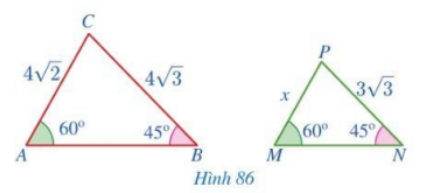
a) Chứng minh \(\Delta MNP \backsim \Delta ABC\)
b) Tìm \(x\).
-
Bài 2 trang 85 SGK Toán 8 Tập 2 Cánh diều - CD
Cho hai tam giác ABC và PMN thỏa mãn \(\widehat A = 70^\circ ,\,\,\widehat B = 80^\circ ,\,\,\widehat M = 80^\circ ,\,\,\widehat N = 30^\circ \). Chứng minh \(\frac{{AB}}{{PM}} = \frac{{BC}}{{MN}} = \frac{{CA}}{{NP}}\)?
-
Bài 3 trang 85 SGK Toán 8 Tập 2 Cánh diều - CD
Cho tam giác nhọn ABC, hai đường cao AD và BE cắt nhau tại H. Chứng minh:
a) \(\Delta ACD \backsim \Delta BCE\) và \(CA.CE = CB.CD\)
b) \(\Delta ACD \backsim \Delta AHE\) và \(AC.AE = AD.AH\)
-
Bài 4 trang 85 SGK Toán 8 Tập 2 Cánh diều - CD
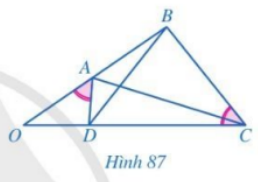
Cho Hình 87 với \(\widehat {OAD} = \widehat {OCB}\). Chứng minh:
a) \(\Delta OAD \backsim \Delta OCB\)
b) \(\frac{{OA}}{{OD}} = \frac{{OC}}{{OB}}\)
c) \(\Delta OAC \backsim \Delta ODB\)
-
Bài 5 trang 85 SGK Toán 8 Tập 2 Cánh diều - CD
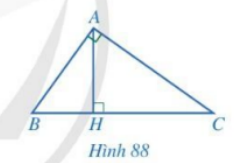
Cho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh:
a) \(\Delta ABC \backsim \Delta HBA\) và \(A{B^2} = BC.BH\)
b) \(\Delta ABC \backsim \Delta HAC\) và \(A{C^2} = BC.CH\)
c) \(\Delta ABH \backsim \Delta CAH\) và \(A{H^2} = BH.CH\)
d) \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\)
-
Bài 6 trang 85 SGK Toán 8 Tập 2 Cánh diều - CD
Trong Hình 89, bạn Minh dùng một dụng cụ để đo chiều cao của cây. Cho biết khoảng cách từ mắt bạn Minh đến cây và đến mặt đất lần lượt là \(AH = 2,8m\) và \(AK = 1,6m\). Em hãy tính chiều cao của cây?







