Bài 3.30 trang 72 SGK Toán 8 Kết nối tri thức tập 1 - KNTT

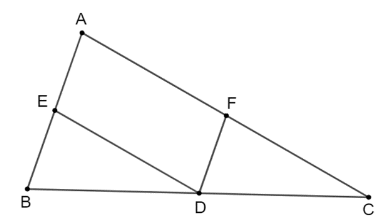
a) Tứ giác AEDF có AE // DF; AF // DE (giả thiết).

Suy ra tứ giác AEDF là hình bình hành.

b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A.

Mà tam giác ABC cân tại A nên đường phân giác AD đồng thời là đường trung tuyến

Do đó D là trung điểm của BC.

Ngược lại, nếu D là trung điểm của cạnh BC của tam giác ABC cân tại A thì hình bình hành AEDF có đường chéo AD là đường phân giác của góc A nên AEDF là hình thoi.

c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì hình bình hành có một góc vuông là hình chữ nhật).

d) Tam giác ABC vuông cân tại A tức là vừa vuông tại A vừa cân tại A.

Theo câu c, nếu ΔABC vuông tại A thì AEDF là hình chữ nhật.

Để hình chữ nhật AEDF là hình vuông thì tức nó cũng là hình thoi.

Theo câu b, AEDF là hình thoi nếu D là trung điểm của cạnh BC của tam giác ABC cân tại A.

Vậy nếu tam giác ABC vuông cân tại A thì để AEDF là hình vuông thì điểm D là trung điểm của BC.

-- Mod Toán 8 HỌC247