Bài tập 3.27 trang 42 SBT Toán 8 Tập 1 Kết nối tri thức
Xét tam giác ABC vuông cân tại A. Lấy trên cạnh BC hai điểm D, E sao cho BD = DE = EC. Lấy các điểm F, G lần lượt thuộc cạnh AC, AB sao cho FE, GD vuông góc với BC. Chứng minh tứ giác DEFG là một hình vuông?
Hướng dẫn giải chi tiết Bài tập 3.27
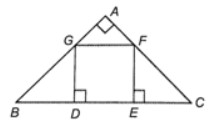
Do ∆ABC vuông cân tại A nên .
Xét ∆GBD vuông tại D và ∆EFC vuông tại E có:
BD = EC;
Do đó ∆GBD = ∆FCE (cạnh góc vuông – góc nhọn kề)
Suy ra
Mà nên
Do đó
Suy ra ∆GBD vuông cân tại D và ∆EFC vuông cân tại E.
Vì vậy GD = BD, EF = EC.
Mà
Suy ra GD = DE = EF.
Do GD ⊥ BC, EF ⊥ BC nên GD // EF
Tứ giác GDEF có GD // EF, GD = EF nên GDEF là hình chữ nhật.
Lại có GD và DE là hai cạnh kề của hình chữ nhật GDEF bằng nhau nên GDEF là hình vuông.
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





