Bài tập 3.24 trang 42 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT

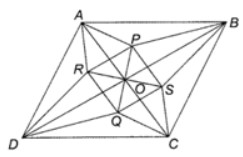
Gọi P, Q lần lượt là giao điểm ba đường phân giác của tam giác OAB, OCD thì O, P, Q thẳng hàng trên đường phân giác của góc AOB .

Do ABCD là hình bình hành nên AB // CD, AD // BC

Suy ra $\widehat{ODC}=\widehat{OBA};\widehat{OCD}=\widehat{OAB}$ (các cặp góc ở vị trí so le trong)

Mà DQ, BP lần lượt là tia phân giác của $\widehat{ODC};\widehat{OBA}$ nên $\widehat{OBP}=\widehat{ODQ}$

Xét ∆OBP và ∆ODQ có:

$\widehat{OBP}=\widehat{ODQ}$; OB = OD; $\widehat{BOP}=\widehat{QOD}$(đối đỉnh)

Do đó ∆OBP = ∆ODQ (g.c.g)

Suy ra OP = OQ, hay O là trung điểm của PQ

Gọi R, S lần lượt là giao điểm ba đường phân giác của tam giác OAD, OBC thì tương tự như trên, ta cũng chứng minh được O là trung điểm của RS và đường thẳng RS là đường phân giác của góc $\widehat{AOD}.$

Do góc AOB và góc AOD là hai góc kề bù nên hai đường phân giác PQ, RS vuông góc với nhau.

Tứ giác PSQR có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau nên là hình thoi.

-- Mod Toán 8 HỌC247