Hướng dẫn Giải bài tập Toán 6 Kết nối tri thức Chương 1 Bài 6 Lũy thừa với số mũ tự nhiên giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
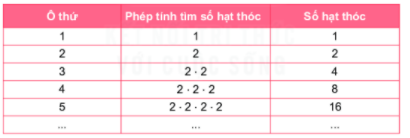
Hoạt động 1 trang 22 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Để tìm số hạt thóc ở ô thứ 8, ta phải thực hiện phép nhân có bao nhiêu thừa số 2?
-
Luyện tập 1 trang 22 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Hoàn thành bảng bình phương của các số tự nhiên từ 1 đến 10.
a
1
2
3
4
5
6
7
8
9
10
a2
?
?
?
?
?
?
?
?
?
?
-
Vận dụng trang 23 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
1) Tính số hạt thóc có trong ô thứ 7 của bàn cờ nói trong bài toán mở đầu.
2) Hãy viết mỗi số tự nhiên sau thành tổng giá trị các chữ số của nó bằng cách dùng các luỹ thừa của 10 theo mẫu:
4 257 = 4 . 103 +2. 102 + 5.10 + 7
a) 23 197
b) 203 184
-
Hoạt động 2 trang 23 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
a) Viết kết quả phép nhân sau dưới dạng một lũy thừa của 7:
72.73 = (7 . 7) . (7 . 7 . 7) = ?
b) Nêu nhận xét về mối liên hệ giữa các số mũ của 7 trong hai thừa số và trong tích tìm được ở câu a).
-
Luyện tập 2 trang 23 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Viết kết quả phép tính dưới dạng một lũy thừa:
a) 53 . 57
b) 24 . 25 . 29
c) 102 . 104 . 106 . 108
-
Hoạt động 3 trang 24 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
a) Giải thích vì sao có thể viết 65 = 63 . 62
b) Sử dụng câu a) để suy ra 65 : 63 = 62. Nêu nhận xét về mối liên hệ giữa các số mũ của 6 trong số bị chia, số chia và thương.
c) Viết thương của phép chia 107 : 104 dưới dạng lũy thừa của 10.
-
Luyện tập 3 trang 24 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Viết kết quả các phép tính dưới dạng một lũy thừa:
a) 76 : 74
b) 1091100 : 1091100
-
Giải bài 1.36 trang 24 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Viết các tích sau dưới dạng một lũy thừa:
a) 9 . 9 . 9 . 9 . 9
b) 10 . 10 . 10 . 10
c) 5 . 5 . 5 . 25
d) a . a . a . a . a . a
-
Giải bài 1.37 trang 24 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Hoàn thành bảng sau vào vở:
Lũy thừa
Cơ số
Số mũ
Giá trị của lũy thừa
43
?
?
?
?
3
5
?
?
2
?
128
-
Giải bài 1.38 trang 24 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Tính:
a) 25
b) 33
c) 52
c) 109
-
Giải bài 1.39 trang 24 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Viết các số sau thành tổng giá trị các chữ số của nó bằng cách dùng các luỹ thừa của 10:
215; 902; 2020; 883 001.
-
Giải bài 1.40 trang 24 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Tính 112, 1112. Từ đó hãy dự đoán kết quả của 1 1112.
-
Giải bài 1.41 trang 24 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Biết 210 = 1024. Tính 29 và 211
-
Giải bài 1.42 trang 24 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Tính:
a) 57. 53
b) 58:54
-
Giải bài 1.43 trang 24 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Ta có: 1 + 3 + 5 = 9 = 32.
Viết các tổng sau dưới dạng bình phương của một số tự nhiên
a) 1 + 3 + 5 + 7;
b) 1 + 3 + 5 + 7 + 9.
-
Giải bài 1.44 trang 24 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Trái Đất có khối lượng khoảng 60 .1020 tấn. Mỗi giây Mặt Trời tiêu thụ 4. 106 tấn khí hydrogen. Hỏi Mặt Trời cần bao nhiêu giây để tiêu thụ một lượng khí hydrogen có khối lượng bằng khối lượng Trái Đất?
-
Giải bài 1.45 trang 24 SGK Toán 6 Kết nối tri thức tập 1 - KNTT
Mỗi giây cơ thể con người trung bình tạo ra khoảng 25.10525.105 tế bào hồng cầu. Hãy tính mỗi giờ có bao nhiêu tế bào hồng cầu đã được tạo ra?
-
Giải bài 1.51 trang 22 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Viết gọn các tích sau bằng cách dùng lũy thừa:
a) 2. 2. 2. 2. 2;
b) 2. 3. 6. 6. 6;
c) 4. 4. 5. 5. 5.
-
Giải bài 1.52 trang 22 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
a) Lập bảng giá trị của 2n2n với n ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10};
b) Viết dưới dạng lũy thừa của 2 các số sau: 8; 256; 1 024; 2 048.
-
Giải bài 1.53 trang 23 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
a) Viết các bình phương của hai mươi số tự nhiên đầu tiên thành một dãy theo thứ tự từ nhỏ đến lớn;
b) Viết các số sau thành bình phương của một số tự nhiên: 64; 100; 121; 169; 196; 289.
-
Giải bài 1.54 trang 23 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
a) Tính nhẩm 10n10n với n ∈ {0; 1; 2; 3; 4; 5}. Phát biểu quy tắc tổng quát tính lũy thừa của 10 với số mũ đã cho;
b) Viết dưới dạng lũy thừa của 10 các số sau: 10; 10 000; 100 000; 10 000 000; 1 tỉ.
-
Giải bài 1.55 trang 23 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Tính:
a) 2525
b) 5252
c) 24.32.724.32.7
-
Giải bài 1.56 trang 23 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Tìm n, biết:
a) 54=n54=n
b) n3=125n3=125
c)11n=133111n=1331
-
Giải bài 1.57 trang 23 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Viết kết quả các phép tính sau dưới dạng một lũy thừa:
a)3.34.353.34.35
b)73:72:773:72:7
c)(x4)3(x4)3
-
Giải bài 1.58 trang 23 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Kết luận sau đúng hay sai?
Không có số chính phương nào có chữ số hàng đơn vị là 2.
-
Giải bài 1.59 trang 23 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Tìm chữ số tận cùng của số 475475 và chứng tỏ số 475+20215475+20215 không phải là số chính phương.
-
Giải bài 1.60 trang 23 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Không tính các lũy thừa, hãy so sánh:
a)27112711 và 818818
b)62556255 và 12571257
c)536536 và 11241124
-
Giải bài 1.61 trang 23 SBT Toán 6 Kết nối tri thức tập 1 - KNTT
Giải thích tại sao ba số sau đều là số chính phương:
a) A = 11 – 2
b) B = 1 111 – 22
c) C = 111 111 – 222






