Bài tập 4 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo
Cho hình tứ diện đều ABCD có cạnh bằng . Gọi I là trung điểm của cạnh CD. Tính khoảng cách giữa hai đường thẳng AC và BI?
Hướng dẫn giải chi tiết Bài tập 4
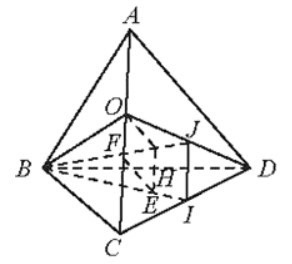
Gọi O là trung điểm AC, J là trung điểm OD.
Vě OH ⊥ BJ, HE // AC, EF // OH.
Có IJ // AC nên AC // (BIJ).
d(AC, BI) = d(AC, (BIJ)) = d(O, (BIJ)).
Do ABCD là tứ diện đều nên ta dễ dàng nhận ra AC ⊥ (OBD).
AC ⊥ OH (OH OBD).
AC // IJ, OH ⊥ IJ.
Kết hợp giả thiết, suy ra OH ⊥ (BIJ) hay d(O, (BIJ)) = OH.
Xét tam giác OBD cân tại O, ta có
.
Áp dụng công thức Heron, ta có:
Ta tính được OH = .
Vậy khoảng cách giữa hai đường thẳng AC và BI là .
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài tập 2 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 5 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 6 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 7 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 8 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 9 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 10 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST





