Bài tập 9 trang 68 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST

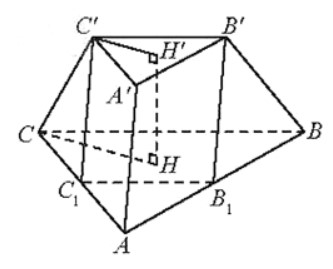
a)

Áp dụng công thức: $V=\frac{1}{3}h\left(S+\sqrt{SS\text{'}}+S\text{'}\right)$ ,

Do ABC, A'B'C' là các tam giác đều nên: \(\left\{ \begin{matrix} S={{S}_{ABC}}={{a}^{2}}\sqrt{3} \\ S'={{S}_{A'B'C'}}=\frac{{{S}_{ABC}}}{4}=\frac{{{a}^{2}}\sqrt{3}}{4} \\ h=2a \\ \end{matrix} \right.\) , thay vào công thức trên ta có:

$V=\frac{1}{3}.2a.\left(a^2\sqrt{3}+\sqrt{a^2\sqrt{3}.\frac{a^2\sqrt{3}}{4}}+\frac{a^2\sqrt{3}}{4}\right)$

$=\frac{2}{3}a.\left(\frac{5\sqrt{3}{a}^2}{4}+\sqrt{\frac{3a^4}{4}}\right)$$=\frac{2}{3}a.\left(\frac{5\sqrt{3}{a}^2}{4}+\frac{\sqrt{3}{a}^2}{2}\right)$

$=\frac{2}{3}a.\left(\frac{5\sqrt{3}{a}^2}{4}+\frac{\sqrt{3}{a}^2}{2}\right)=\frac{2}{3}a.\frac{7\sqrt{3}{a}^2}{4}=\frac{7a^3\sqrt{3}}{6}$.

b)Áp dụng công thức: $V\text{'}=S\text{'}.h\text{'}$ , với $S\text{'}=\frac{a^2\sqrt{3}}{4},h\text{'}=2a.$

Ta có: $V\text{'}=\frac{a^2\sqrt{3}}{4}.2a.=\frac{a^3\sqrt{3}}{2}$ .

-- Mod Toán 11 HỌC247