Bài tập 31 trang 100 SBT Toán 11 Tập 2 Cánh diều - CD

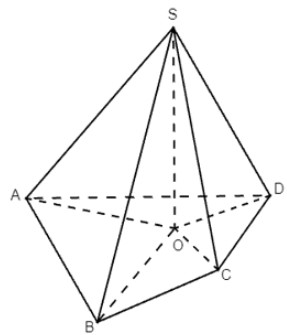
Gọi O là hình chiếu của S trên (ABCD) hay SO ⊥ (ABCD).

Mà OA, OB, OC, OD đều nằm trên (ABCD) nên SO ⊥ OA, SO ⊥ OB, SO ⊥ OC, SO ⊥ OD.

Suy ra: bốn tam giác SAO, SBO, SCO, SDO vuông tại O nên các góc $\widehat{SAO}$, $\widehat{SBO}, \widehat{SCO,}$$\widehat{SDO}$ đều lớn hơn 0° và nhỏ hơn 90°.

Vì O là hình chiếu của S trên (ABCD), ta suy ra: ${\alpha }_1=\widehat{SAO}$ và 0° < α₁ < 90°.

Xét tam giác SAO vuông tại O có: $\sin {\alpha }_1=\sin \widehat{SAO}=\frac{SO}{SA}$.

Chứng minh tương tự, ta cũng có:

· $\sin {\alpha }_2=\sin \widehat{SBO}=\frac{SO}{SB}$ (0° < α₂ < 90°).

· $\sin {\alpha }_3=\sin \widehat{SCO}=\frac{SO}{SC}$ (0° < α₃ < 90°).

·$\sin {\alpha }_4=\sin \widehat{SDO}=\frac{SO}{SD}$ (0° < α₄ < 90°).

Như vậy: SA = SB = SC = SD $\iff \frac{SO}{SA}=\frac{SO}{SB}=\frac{SO}{SC}=\frac{SO}{SD}$

⇔ sinα₁ = sinα₂ = sinα₃ = sinα₄

⇔ α₁ = α₂ = α₃ = α₄ (vì 0° < α₁ < 90°; 0° < α₂ < 90°; 0° < α₃ < 90°; 0° < α₄ < 90°)

Vậy SA = SB = SC = SD ⇔ α₁ = α₂ = α₃ = α₄.

-- Mod Toán 11 HỌC247