Bài tập 7.24 trang 34 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT

Ta có \(SO \bot BD,CO \bot BD\) nên góc nhị diện \(\left[ {S,BD,C} \right]\) bằng \(\widehat {SOC}\).

Vì tam giác \(SAO\) vuông tại \(A\) nên:

\(SO = \sqrt {S{A^2} + A{O^2}} = \frac{{a\sqrt 6 }}{2}\) và \({\rm{cos}}\widehat {SOC} = - {\rm{cos}}\widehat {SOA} = - \frac{{OA}}{{SO}} = - \frac{{\sqrt 3 }}{3}\).

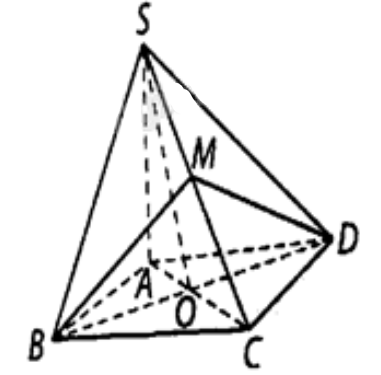
Kẻ \(BM \bot SC\) tại \(M\) thì \(DM \bot SC\) nên \(\left[ {B,SC,D} \right] = \widehat {BMD}\).

Ta có: \(BC \bot \left( {SAB} \right)\) nên tam giác \(SBC\) vuông tại \(B\).

Tính được \(SB = a\sqrt 2 \), \(SC = a\sqrt 3 \) và \(DM = BM = \frac{{SB \cdot BC}}{{SC}} = \frac{{a\sqrt 6 }}{3}\).

Áp dụng định lí côsin trong tam giác \(BDM\), ta có:

\({\rm{cos}}\widehat {BMD} = \frac{{B{M^2} + D{M^2} - B{D^2}}}{{2 \cdot BM \cdot DM}} = - \frac{3}{4}\).

-- Mod Toán 11 HỌC247