Giải bài 6.6 trang 8 SBT Toán 10 Kết nối tri thức tập 2 - KNTT

Phương pháp giải

+ Đỗ thị của một hàm số đồng biến trên khoảng (a; b) là đường “đi lên” từ trái sang phải;

+ Đồ thị của một hàm số nghịch biến trên khoảng (a; b) là đường "đi xuống" từ trái sang phải.

Lời giải chi tiết

a) \(y =  - \frac{1}{2}x + 5\)

Đồ thị hàm số \(y =  - \frac{1}{2}x + 5\) là đường thẳng đi qua 2 điểm A(0; 5) và B\(\left( {10;0} \right)\)

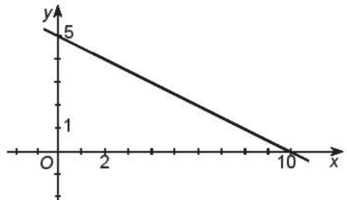
Từ đồ thị ta có:

  +) Tập giá trị: \(\mathbb{R}\)

  +) Hàm số nghịch biến trên \(\mathbb{R}\)

b) \(y = 3{x^2}\)

Đồ thị hàm số \(y = 3{x^2}\) là đường parabol có bề lõm quay lên trên và đỉnh là gốc tọa độ O

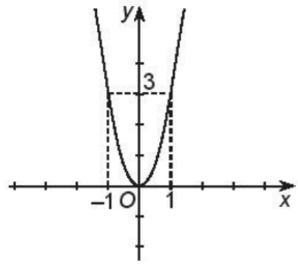
Từ đồ thị ta có:

+) Tập giá trị: \({\rm{[}}0; + \infty )\)

+) Hàm số nghịch biến trên \(( - \infty ;0)\) và đồng biến trên \((0; + \infty )\)

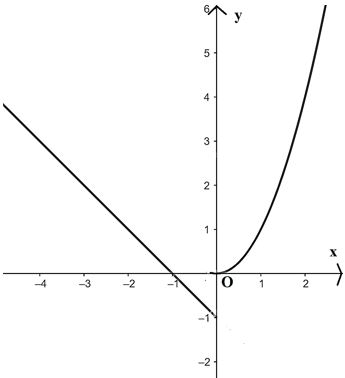
c) \(y = \left\{ \begin{array}{l}{x^2},x \ge 0\\ - x - 1,x < 0\end{array} \right.\)

Ta có đồ thị sau:

Từ đồ thị ta có:

+) Tập giá trị: \(( - 1; + \infty )\)

+) Hàm số nghịch biến trên \(( - \infty ;0)\) và đồng biến trên \((0; + \infty )\)

-- Mod Toán 10 HỌC247