Giải bài tập 32.10 trang 67 SBT Tin học 10 Kết nối tri thức - KNTT

Phương pháp giải:

Bài toán này nằm trong Chương trình môn Vật lí 10, phần chuyển động ném xiên của vật thể.

Lời giải chi tiết:

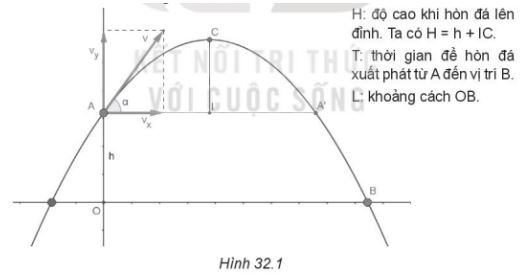
Quan sát hình sau. Hòn đá được ném lên từ vị trí A có độ cao h với góc ném a và vận tốc góc v. Quỹ đạo chuyển động của hòn đá sẽ có dạng parabol như trong Hình 32.1. Hòn đá sẽ lên đỉnh cao nhất tại c và sau đó chạm đất tại vị trí B. Em cần tính ba thông số H, T, L như sau:

Sơ lược cách tính các tham số H, T, L.

Lực ném v sẽ phân tích thành 2 lực: lực thẳng đứng vy và lực ngang vx. Ta có công thức:

vx = v.cos(a), vy = v.sin(d) (1)

Phương trình tham số theo thời gian t của quỹ đạo hòn đá chuyển động như sau:

\(\left\{ \begin{array}{l}
x(t) = {v_x}t\\
y(t) = h + {v_y}t - \frac{{g{t^2}}}{2}(2)
\end{array} \right.\)

Thời gian t trong công thức (2) tính từ 0, tức là từ điểm A. g = 9.8 là trọng lực Trái Đất.

Để tính thời gian T chúng ta giải phương trình y(t) = 0 trong công thức (2). Đây là phương trình bậc hai với t. T chính là nghiệm dương của phương trình này. Khoảng cách L dễ dàng tính được theo công thức L = vxT.

Để tính độ cao H thì khó hơn.

Thời gian để hòn đá bay đến điểm A’ được tính như sau:

y(t) = h, tức là vyt - = 0, từ đó suy ra t = 2vy/g. Thời gian đi đến đỉnh C bằng một nửa thời gian đến A, vậy suy ra thời gian đạt đỉnh cao nhất là:

t= vy/g = v.sin(a)/g (3)

Từ công thức (3) dễ dàng tính được độ cao IC, từ đó tính được H.

Từ các phân tích trên chúng ta sẽ tính được các công thức sau cho T, H và L.

\(\begin{array}{l}
T = \frac{{v\sin \left( \alpha  \right) + \sqrt {v{}^2 + {{\sin }^2}\left( \alpha  \right) + 2hg} }}{g}(4)\\
H = h + \frac{{v{}^2 + {{\sin }^2}\left( \alpha  \right)}}{{2g}}(5)\\
L = \frac{{v{}^2 + \sin \left( {2\alpha } \right)}}{{2g}} + v\cos (\alpha )\frac{{\sqrt {v{}^2 + {{\sin }^2}\left( \alpha  \right) + 2hg} }}{g}(6)
\end{array}\)

Để tính theo các công thức (4), (5), (6) cần sử dụng các hàm số toán học như sin, cosin, hàm tính căn bậc hai. Các hàm toán học không có sẵn trong Python mà có trong một module độc lập bên ngoài, module math. Muốn sử dụng các hàm số này chúng ta cần đưa lệnh sau vào chương trình (ở dòng lệnh đầu tiên).

from math import

Muốn dùng tất cả các hàm có trong module math (hay bất kì module nào khác) chúng ta dùng lệnh: from math import *

Các hàm lượng giác sin(a), cos(a) trong Python quy định tham số góc đầu vào không tính theo độ, mà theo độ đo radian. Do vậy chúng ta cần thêm một hàm số nữa là hàm radians() dùng để chuyển số đo từ độ sang radian.

Vậy chương trình sẽ cần các hàm toán học sau.

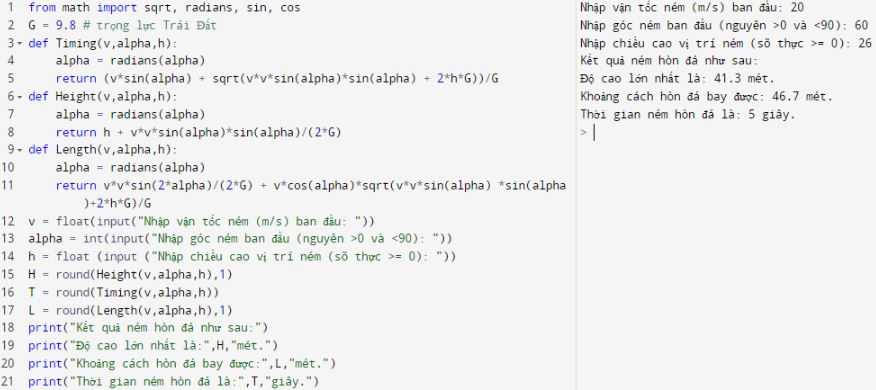
from math import sqrt, radians, sin, cos

Chương trình cần được tạo với tên flyingrocket.py và phần nội dung chính mô tả ba hàm số Timing(), Height() và Length(). Các hàm này có tham số đầu vào là v, alpha, h và có giá trị trả lại chính là T, H, L mà chúng ta cần tìm.

-- Mod Tin Học 10 HỌC247