Hoạt động trang 8 SGK Vật lí 11 Kết nối tri thức
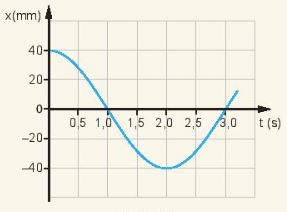
Đồ thị li độ - thời gian của một con lắc đơn dao động điều hoà được mô tả trên Hình 1.3.
Hình 1.3
1. Hãy mô tả dao động điều hoà của con lắc đơn.
2. Xác định biên độ và li độ của con lắc ở các thời điểm t = 0, t = 0,5s, t = 2,0s.
Hướng dẫn giải chi tiết Hoạt động trang 8
Phương pháp giải:
1. Vận dụng kiến thức đã học trong phần 1. Đồ thị dao động điều hoà.
2. Để tìm li độ tại thời điểm t ta thay t vào phương trình dao động hoặc quan sát đồ thị.
Lời giải chi tiết:
1. Từ đồ thị ta thấy:
- Biên độ dao động là giá trị lớn nhất của li độ: A = xmax = 40 (cm).
- Từ vị trí cao nhất đến vị trí thấp nhất gần mất thời gian là một nửa chu kì nên ta có:
\(\frac{T}{2} = 2\left( s \right) \Rightarrow T = 4\left( s \right)\)
- Tần số góc của con lắc là: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{4} = \frac{\pi }{2}\)
- Lúc t = 0, con lắc đang ở vị trí biên dương: x = A = 40cm.
\(x = Acos\varphi \Leftrightarrow cos\varphi = \frac{x}{A} = 1 \Rightarrow \varphi = 0\)
Vậy phương trình dao động: \(x = 40\cos \left( {\frac{\pi }{2}t} \right)\)
2.
- Lúc t = 0, con lắc đang ở vị trí biên dương: x = A = 40cm.
- Lúc t = 0,5s,li độ của con lắc là:
\(x = 40\cos \left( {\frac{\pi }{2}.0,5} \right) = 40.\cos \frac{\pi }{4} = 20\sqrt 2 \left( {cm} \right)\)
- Lúc t = 1s, quan sát trên đồ thị li độ con lắc là: x = 0.
- Lúc t = 2s, li độ của con lắc là x = −A = −40cm.
-- Mod Vật Lý 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.