Bộ 5 đề thi HKII năm 2021 môn Toán 11 - Trường THPT Thủ Đức

TRƯỜNG THPT THỦ ĐỨC

ĐỀ THI HKII NẮM HỌC 2021 MÔN: TOÁN 11 Thời gian: 90 phút

 

I. PHẦN TRẮC NGHIỆM (6 điểm)

Câu 1: Cho \(\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)=-\infty \), kết quả của \(\underset{x\to a}{\mathop{\lim }}\,\left( -3.f\left( x \right) \right)\) bằng

A. \(+\infty \) .                 B. \(-\infty \)                   C. 0.                                 D. 3.

Câu 2: Cho hình chóp đều S.ABCD có AB=a, góc giữa cạnh bên và mặt đáy bằng \(30{}^\circ \) (tham khảo hình vẽ). Độ dài đường cao hình chóp S.ABCD bằng

A. \(\frac{a\sqrt{6}}{3}\).                                        B. \(\frac{\sqrt{6}}{6}\). 

C. \(\frac{a\sqrt{6}}{6}\).                                        D. \(a\sqrt{2}\).

Câu 3: Container của xe tải dùng để chở hàng hóa thường có dạng hình hộp chữ nhật. Chúng ta mô hình hóa thùng container bằng hình hộp chữ nhật MNPQ.EFGH (tham khảo hình vẽ bên dưới). Chọn khẳng định sai khi nói về hai đường thẳng vuông góc trong các khẳng định sau.

 

A. \(HE\bot MN\).           B. \(HE\bot QN\).            C. \(HE\bot GP\).            D. \(HE\bot NF\).

Câu 4: Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình bên. Kết quả của \(\underset{x\to -\infty }{\mathop{\lim }}\,f\left( x \right)\) bằng

A. \(+\infty \).                  B. \(-\infty \).                  

C. 1.                                 D. 2.

Câu 5: Mệnh đề nào sau đây SAI?

A. \(\lim \left( 2n+1 \right)=+\infty \).                     B. \(\lim \frac{n-1}{n+1}=1\).          

C. \(\lim \frac{n+3}{{{n}^{2}}+1}=0\).                   D. \(\lim \frac{1}{2n+1}=\frac{1}{2}\).

Câu 6: Cho hàm số \(y=2{{x}^{2}}-x+1\) có đồ thị (C). Tiếp tuyến tại điểm M(1; 2) của (C) có phương trình

A. y=2.                        B. y=4x-2.                   C. y=3x-5.                   D. y=3x-1.

Câu 7: Kết quả của \(\underset{x\to -\infty }{\mathop{\lim }}\,{{x}^{5}}\) bằng

A. \(-\infty \).                   B. 5.                                 C. 0.                                 D. \(+\infty \).

Câu 8: \(\underset{x\to +\infty }{\mathop{\lim }}\,\frac{x-2}{x+3}\) bằng.

A. 2.                                 B. \(-\frac{2}{3}\).           C. 1.                                 D. -3.

Câu 9: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a; Gọi M là trung điểm của SD (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng

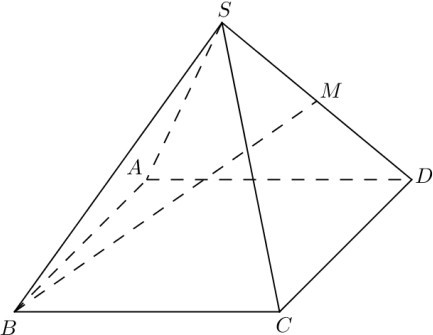
A. \(\frac{\sqrt{3}}{2}.\)                B. \(\frac{\sqrt{2}}{2}.\)                     C. \(\frac{2}{3}.\)                    D. \(\frac{1}{3}.\)

Câu 10: Cho đường thẳng a không vuông góc với mặt phẳng \(\left( P \right)\). Khi đó, góc giữa a và mặt phẳng \(\left( P \right)\) là góc giữa

A. a và đường thẳng bất kì nằm trong \(\left( P \right)\)        

B. a và hình chiếu vuông góc của a lên \(\left( P \right)\)

C. a và đường vuông góc với \(\left( P \right)\).    

D. a và một đường thẳng bất kì cắt \(\left( P \right)\).

ĐÁP ÁN

1	A	6	C
2	C	7	A
3	D	8	C
4	C	9	D
5	D	10	B

...

---(Nội dung đầy đủ, chi tiết phần đáp án của đề thi số 1 vui lòng xem tại online hoặc đăng nhập để tải về máy)---

Câu I. (2,0 điểm)

a) Tính giới hạn sau: \(I=\underset{x\to 4}{\mathop{\lim }}\,\frac{\sqrt{x-3}-1}{{{x}^{2}}-3x-4}\)

b) Cho hàm số: \(f\left( x \right)={{\sin }^{3}}\left( \frac{\pi }{3}-x \right)\). Tính \(f'\left( \pi  \right)\).

Câu II. (2,0 điểm). Tìm a để hàm số sau liên tục trên R:

\(f\left( x \right)=\left\{ \begin{align} & \frac{{{x}^{3}}-{{x}^{2}}+2x-2}{x-1};\,\,khi\,x\ne 1 \\ & 2x+a\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,x=1 \\ \end{align} \right.\)

Câu III. (2,0 điểm) Cho hàm số : \(y=\frac{2x-1}{x+1}\,\).

a) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng -2.

b) Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với đường thẳng \(d:\,\,3x-y-7=0\).

Câu IV. (3,0 điểm) Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên \(SA=a\sqrt{2}\) và vuông góc với mặt đáy.

a) Chứng minh rằng \(\left( SAB \right)\bot \left( SBC \right)\).

b) Tính góc giữa đường thẳng SC và \(mp\left( SAB \right)\).

c) Tính khoảng cách giữa hai đường thằng SD và AC.

Câu V. (1,0 điểm). Cho hàm số \(y=\frac{2x-1}{x+1}\). Tìm tọa độ điểm M thuộc đồ thị sao cho khoảng cách từ điểm I(-1;2) tới tiếp tuyến của đồ thị tại M là lớn nhất.

...

---(Nội dung đầy đủ, chi tiết phần đáp án của đề thi số 2 vui lòng xem tại online hoặc đăng nhập để tải về máy)---

Câu 1: Tính \(\underset{{}}{\mathop{\lim }}\,(\sqrt{2}+\frac{\sqrt{2}}{2}+...+\frac{\sqrt{2}}{{{2}^{n}}})\):

A. \(\frac{\sqrt{2}}{2}+\sqrt{2}\)

B. \(\frac{1}{2}+\sqrt{2}\)

C. \(2\sqrt{2}\)

D. \(\frac{1}{2}\)

Câu 2: Tính \(\underset{x\to +\infty }{\mathop{\lim }}\,\frac{3-2x-5{{x}^{3}}}{{{x}^{3}}-1}\):

A. \(-\infty \)                    B. -5                                 C. 5                                  D. 3

Câu 3: Cho tứ diện ABCD có \(SA\bot (BCD)\),G là trọng tâm của tam giác ACD, M là trung điểm của CD. Gọi G’ là hình chiếu của G lên mặt phẳng (BCD). Khi đó tỉ số \(\frac{G'M}{G'B}\) bằng:

A. 2                              B. \(\frac{1}{3}\)              C. \(\frac{2}{3}\)              D. \(\frac{1}{2}\)

Câu 4: Cho hàm số \(f\left( x \right)=\left\{ \begin{align} & \frac{\sqrt{x+3}-2}{x-1}\text{ khi }x>1\text{ } \\ & {{m}^{2}}x+3m+\frac{1}{4}\text{ khi }x\le 1 \\ \end{align} \right.\). Giá trị m để \(f\left( x \right)\) liên tục tại x = 1 là:

A. m=0

B. m=-3

C. m=0 hoặc m=-3

D. Đáp án khác

Câu 5: Cho hàm số \(f\left( x \right)=\left\{ \begin{align} & {{x}^{2}}-ax,\text{ khi }x\ge 1 \\ & \frac{{{x}^{2}}-1}{x-1}\text{ khi }x<1 \\ \end{align} \right.\). Tìm a để hàm số có giới hạn tại x=1

A. -1                            B. 1                                  C. 0                                  D. không tồn tại a

Câu 6: Biết \(\underset{x\to 1}{\mathop{\lim }}\,\frac{\sqrt{{{x}^{2}}+x+2}-\sqrt[3]{7x+1}}{\sqrt{2}\left( x-1 \right)}=\frac{a\sqrt{2}}{b}\) ( \(a,b\in \mathbb{Z}\) và \(\frac{a}{b}\) tối  giản). Giá trị của a + b = ?

A. 51                                B. 13                                C. 5                                  D. 37

Câu 7: Chọn kết quả đúng của \(\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\frac{x+3}{{{x}^{2}}-4x+3}\):

A. 1                                  B. 0                                  C. \(+\infty \)                   D. \(-\infty \)

Câu 8: Hàm số nào trong các hàm số dưới đây liên tục tại điểm x=2

A. \(y={{x}^{5}}+8{{x}^{3}}-x+1.\)                         B. \(y=\frac{x+2}{x-2}.\)

C. \(y=\frac{1}{{{x}^{2}}-4}.\)                                             D. \(y=\sqrt{x-3}\)

Câu 9: Đạo hàm của biểu thức \(f(x)=({{x}^{2}}-3)\sqrt{{{x}^{2}}-2x+4}\) là:

A. \(f'(x)=2x\frac{(x-1)({{x}^{2}}-3)}{\sqrt{{{x}^{2}}-2x+4}}\)

B. \(f'(x)=2x\sqrt{{{x}^{2}}-2x+4}+\frac{(x-1)({{x}^{2}}-3)}{\sqrt{{{x}^{2}}-2x+4}}\)

C. \(f'(x)=2x\sqrt{{{x}^{2}}-2x+4}+\frac{({{x}^{2}}-3)}{2\sqrt{{{x}^{2}}-2x+4}}\)

D. \(f'(x)=(2x-3)\sqrt{{{x}^{2}}-2x+4}+\frac{(x-1)({{x}^{2}}-3)}{\sqrt{{{x}^{2}}-2x+4}}\)

Câu 10: Hàm số nào dưới đây gián đoạn tại x=-1:

A. \(y=\frac{x+1}{x-1}\)

B. \(y=\frac{x-1}{x+1}\)

C. \(y={{x}^{2}}-x+1.\)

D. \(y=\frac{1}{{{x}^{2}}+1}\)

ĐÁP ÁN

1	2	3	4	5	6	7	8	9	10
C	B	D	C	A	B	C	A	B	B

...

---(Nội dung đầy đủ, chi tiết phần đáp án của đề thi số 3 vui lòng xem tại online hoặc đăng nhập để tải về máy)---

A. PHẦN TRẮC NGHIỆM (5 điểm)

Câu 1. Giới hạn \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {x + 1}  - 1}}{x}\) bằng

A.  2.                                      B.  3.

C.  \(\frac{1}{2}\).                D.  -2.

Câu 2. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi tâm \(O\). Biết \(SA = SC,\,SB = SD\). Tìm khẳng định sai ?

A.  \(BD \bot (SAC).\)

B.  \(CD \bot AC.\)

C.  \(SO \bot (ABCD).\)

D.  \(AC \bot (SBD).\)

Câu 3. Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 3x + 2}}{{x - 2}}\,\,\,\,khi\,\,\,x \ne 2\\m\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,x = 2\end{array} \right..\) Tìm tất cả các giá trị của tham số \(m\) để hàm số đã cho liên tục tại \({x_0} = 2.\)

A.  \(m =  - 2.\)

B.  \(m = 1.\)

C.  \(m =  \pm \sqrt 2 .\)

D.  \(m = 2.\)

Câu 4. Tiếp tuyến của đồ thị hàm số \(y = \frac{{{x^3}}}{3} - {x^2} - 2x\) có hệ số góc \(k =  - 3\) có phương trình là

A.  \(y =  - 3x + \frac{1}{3}.\)

B.  \(y =  - 3x - \frac{1}{3}.\)

C.  \(y =  - 9x + 43.\)

D.  \(y =  - 3x - 11.\)

Câu 5. Cho hàm số \(f(x) = \frac{1}{3}{x^3} + \frac{1}{2}{x^2} - 12x - 1\). Giải phương trình \(f'(x) = 0\).

A.  \(\left\{ { - 4;3} \right\}\)

B.  \(\left[ { - 3;4} \right]\).

C.  \(\left[ { - 4;3} \right]\).

D.  \(\left( { - \infty ; - 3} \right] \cup \left[ {4; + \infty } \right)\).

Câu 6. Cho các hàm số \(u = u(x),v = v(x)\). Trong các công thức sau, công thức nào sai?

A. \(\left( {u.v} \right)' = u'.v - u.v'\)

B.  \(\left( {\frac{u}{v}} \right)' = \frac{{u'.v - u.v'}}{{{v^2}}},\)\(v = v(x) \ne 0\)

C.  \(\left( {u + v} \right)' = u' + v'\)

D.  \(\left( {u - v} \right)' = u' - v'\)

Câu 7. Đạo hàm của hàm số \(y = {x^4} + 3{x^2} - x + 1\) là

A.  \(y' = 4{x^3} - 6{x^2} + x\).

B.  \(y' = 4{x^3} + 3{x^2} - x\).

C.  \(y' = 4{x^3} + 6x - 1\).

D.  \(y' = 4{x^3} - 6x + 1\).

Câu 8. Giới hạn\(\mathop {\lim }\limits_{x \to {1^ - }} \frac{5}{{x - 1}}\) bằng

A.  2.                                      B.  \( - 5\).

C.  \( - \infty \).                      D.  \( + \infty \).

Câu 9. Đạo hàm của hàm số \(y = \frac{{2x + 1}}{{x - 1}}\) là

A.  \(y' =  - \frac{3}{{{{\left( {x + 1} \right)}^2}}}\)

B.  \(y' =  - \frac{3}{{{{\left( {x - 1} \right)}^2}}}\).

C.  \(y' = \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}}\).

D.  \(y' = \frac{3}{{{{\left( {x + 1} \right)}^2}}}\).

Câu 10. Cho hàm số \(f(x) = {\left( {{x^2} - 3x} \right)^2}\). Tính \(f'(1)\).

A.  \(4\).                                 B.  \( - 12\).

C.  \(1\).                                 D.  \( - 1\).

ĐÁP ÁN

1C	2B	3B	4A	5A
6A	7C	8C	9B	10A

---(Nội dung đầy đủ, chi tiết phần đáp án của đề thi số 4 vui lòng xem tại online hoặc đăng nhập để tải về máy)---

I. PHẦN TRẮC NGHIỆM (7 điểm)

Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(SA\bot \left( ABCD \right)\). Trong các tam giác sau tam giác nào không phải là tam giác vuông?

A. \(\Delta \text{SBC}\)

B. \(\Delta \text{SAB}\)

C. \(\Delta \text{SCD}\)

D. \(\Delta \text{SBD}\)

Câu 2: Dãy số nào sau đây có giới hạn bằng 0?

A. \(\frac{\sqrt{2{{n}^{2}}-1}}{5n+3{{n}^{2}}}\)

B. \(\frac{1-2{{n}^{2}}}{5n+3{{n}^{2}}}\)

C. \({{u}_{n}}=\frac{{{n}^{2}}-2n}{5n+3}\)

D. \({{u}_{n}}=\frac{{{n}^{2}}-2}{\sqrt{1+3{{n}^{2}}}}\)

Câu 3: Khẳng định nào sau đây là đúng?

A. Hàm số \(f(x)=\frac{x-1}{x+1}\) gián đoạn tại x=1

B. Hàm số \(f(x)=\frac{x+1}{{{x}^{2}}+1}\) liên tục trên R

C. Hàm số \(f(x)=\frac{{{x}^{2}}-1}{x+1}\) liên tục trên R

D. Hàm số \(f(x)=\frac{x+1}{x-1}\) liên tục trên (0;2)

Câu 4: Giới hạn \(\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\frac{2x+3}{1-x}\) là:

A. \(-\infty \)                    B. 2                              C. \(+\infty \)                   D. -2

Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC. Khẳng định nào sau đây đúng ?

A. \(SO\bot (ABCD)\)

B. \(BD\bot (SAC)\)

C. \(AC\bot (SBD)\)

D. \(AB\bot (SAD)\)

Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng ?

A. \((SCD)\bot (SAD)\)

B. \((SBC)\bot (SAC)\)

C. \((SDC)\bot (SAC)\)

D. \((SBD)\bot (SAC)\)

Câu 7: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \((SAB)\bot (ABC)\), SA = SB ,  I là trung điểm AB. Khẳng định nào sau đây sai ?

A. Góc giữa SC và \((ABC)\) là \(\widehat{SCI}\)

B. \(SI\bot (ABC)\)

C. \(AC\bot (SAB)\)

D. \(AB\bot (SAC)\)

Câu 8: Một chất điểm chuyển động có phương trình \(s={{t}^{3}}+3t\) (t tính bằng giây, s tính bằng mét) Tính vận tốc của chất điểm tại thời điểm \({{t}_{0}}=2\) (giây) ?

A. 15m/s                     B. 7m/s                        C. 14m/s                     D. 12m/s

Câu 9: Cho một hàm số y = f(x). Khẳng định nào sau đây là đúng?

A. Nếu f(a)f(b) <0 thì phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (a;b).

B. Nếu hàm số f(x) liên tục, đồng biến trên đoạn [a;b] và f(a)f(b) > 0 thì phương trình f(x) = 0 không có nghiệm trong khoảng (a;b).

C. Nếu f(x) liên tục trên đoạn [a;b], f(a)f(b) < 0 thì phương trình f(x) = 0 không có nghiệm trên khoảng (a;b).

D. Nếu phương trình f(x) = 0 có nghiệm trong khoảng (a;b) thì hàm số f(x) phải liên tục trên khoảng (a;b)

Câu 10: \(\lim \left( {\sqrt {{n^2} + 3n}  - \sqrt {{n^2} + 2} } \right)\) ( \(a,b \in Z\) và \(\frac ab\) tối giản) thì tổng a² + b² là :

A. 10                                B. 3                                  C. 13                                D. 20

ĐÁP ÁN

1D

2A

3B

4C

5C

6A

7D

8A

9B

10C

---(Nội dung đầy đủ, chi tiết phần đáp án của đề thi số 5 vui lòng xem tại online hoặc đăng nhập để tải về máy)---

Trên đây là một phần trích dẫn nội dung Bộ 5 đề thi HKII năm 2021 môn Toán 11 - Trường THPT Thủ Đức. Để xem toàn bộ nội dung các em đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.

Ngoài ra các em có thể tham khảo thêm một số tư liệu cùng chuyên mục tại đây:

• Bộ 5 đề thi HKII năm 2021 môn Toán 11 - Trường THPT Nguyễn Du

Chúc các em học tốt!