Giải bài 1.2 tr 156 sách BT Toán lớp 8 Tập 1
a. Cho tam giác đều ABC. Gọi M,N,P tương ứng là trung điểm của các cạnh BC, CA, AB. Chứng minh MNP là tam giác đều.
b. Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh BC, CD, DA, AB. Chứng minh MNPQ là hình vuông (tứ giác đều)
c. Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.
Hướng dẫn giải chi tiết
Hướng dẫn giải
a. Áp dụng tính chất đường trung bình của tam giác
b. Áp dụng tính chất hai tam giác bằng nhau
c. Để chứng minh \(MNPQR\) là ngũ giác đều ta cần chứng minh hai điều: hình đó có tất cả các cạnh bằng nhau và có tất cả các góc bằng nhau.
Lời giải chi tiết
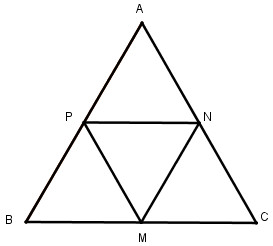
a. Ta có: M là trung điểm của BC
N là trung điểm của AC
nên MN là đường trung bình của ∆ ABC ⇒ MN = \({1 \over 2}\)AB
Ta có: P là trung điểm của AB nên MP là đường trung bình của ∆ ABC
⇒ MP = \({1 \over 2}\)AC
NP là đường trung bình của ∆ ABC ⇒ NP = \({1 \over 2}\)BC
mà AB = BC = AC (gt) ⇒ MN = MP = NP. Vậy ∆ MNP đều
b.
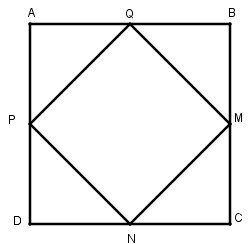
Xét ∆ APQ và ∆ BQM:
AQ = BQ (gt)
\(\widehat A = \widehat B = {90^0}\)
AP = BM (gt)
Do đó: ∆ APQ = ∆ BQM (c.g.c) ⇒ PQ = QM (1)
Xét ∆ BQM và ∆ CMN:
BM = CM (gt)
\(\widehat B = \widehat C = {90^0}\)
BQ = CN (gt)
Do đó: ∆ BQM = ∆ CMN (c.g.c) ⇒ QM = MN (2)
Xét ∆ CMN và ∆ DNP:
CN = DN (gt)
\(\widehat C = \widehat D = {90^0}\)
CM = DP (gt)
Do đó: ∆ CMN = ∆ DNP (c.g.c) ⇒ MN = NP (3)
Từ (1), (2) và (3) uy ra: MN = NP = PQ = QM
nên tứ giác MNPQ là hình thoi
Vì AP = AQ nên ∆ APQ vuông cân tại A
BQ = BM nên ∆ BMQ vuông cân tại B
\( \Rightarrow \widehat {AQP} = \widehat {BQM} = {45^0}\)
\(\widehat {AQP} + \widehat {PQM} + \widehat {BQM} = {180^0}\) (kề bù)
\( \Rightarrow \widehat {PQM} = {180^0} - \left( {\widehat {AQP} + \widehat {BQM}} \right)\)
\(= {180^0} - \left( {{{45}^0} + {{45}^0}} \right) = {90^0}\)
Vậy tứ giác MNPQ là hình vuông.
c.
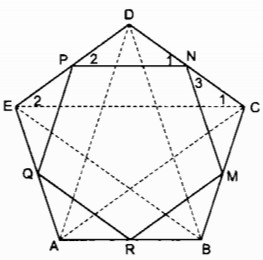
Xét ∆ ABC và ∆ BCD:
AB = BC (gt)
\(\widehat B = \widehat C\) (gt)
BC = CD (gt)
Do đó: ∆ ABC = ∆ BCD (c.g.c)
⇒ AC = BD (1)
Xét ∆ BCD và ∆ CDE:
BC = CD (gt)
\(\widehat C = \widehat D\) (gt)
CD = DE (gt)
Do đó: ∆ BCD = ∆ CDE (c.g.c) ⇒ BD = CE (2)
Xét ∆ CDE và ∆ DEA:
CD = DE (gt)
\(\widehat D = \widehat E\) (gt)
DE = EA (gt)
Do đó: ∆ CDE = ∆ DEA (c.g.c) ⇒ CE = DA (3)
Xét ∆ DEA và ∆ EAB:
DE = EA (gt)
\(\widehat E = \widehat A\) (gt)
EA = AB (gt)
Do đó: ∆ DEA = ∆ EAB (c.g.c) ⇒ DA = EB (4)
Từ (1), (2), (3), (4) uy ra: AC = BD = CE = DA = EB
Trong ∆ ABC ta có RM là đường trung bình
⇒ RM = \({1 \over 2}\)AC (tính chất đường trung bình của tam giác)
Mặt khác, ta có: Trong ∆ BCD ta có MN là đường trung bình
⇒ MN = \({1 \over 2}\)BD (tính chất đường trung bình của tam giác)
Trong ∆ CDE ta có NP là đường trung bình
⇒ NP = \({1 \over 2}\)CE (tính chất đường trung bình của tam giác)
Trong ∆ 9DEA ta có PQ là đường trung bình
⇒ PQ = \{1 \over 2}\)DA (tính chất đường trung bình của tam giác)
Trong ∆ EAB ta có QR là đường trung bình
⇒ QR = \({1 \over 2}\)EB (tính chất đường trung bình của tam giác)
uy ra: MN = NP = PQ = QR = RM
Ta có: \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E = {{\left( {5 - 2} \right){{.180}^0}} \over 5} = {108^0}\)
∆ DPN cân tại D
\( \Rightarrow \widehat {DPN} = \widehat {DNP} = {{{{180}^0} - \widehat D} \over 2} = {{{{180}^0} - {{108}^0}} \over 2} = {36^0}\)
∆ CNM cân tại C
\( \Rightarrow \widehat {CNM} = \widehat {CMN} = {{{{180}^0} - \widehat C} \over 2} = {{{{180}^0} - {{108}^0}} \over 2} = {36^0}\)
\(\widehat {ADN} + \widehat {PNM} + \widehat {CNM} = {180^0}\)
\( \Rightarrow \widehat {PNM} = {180^0} - \left( {\widehat {ADN} + \widehat {CNM}} \right)\)
\(= {180^0} - \left( {{{36}^0} + {{36}^0}} \right) = {108^0}\)
∆ BMR cân tại B
\(\eqalign{ & \Rightarrow \widehat {BMR} = \widehat {BRM} = {{180^\circ - \widehat B} \over 2} = {{180^\circ - 108^\circ } \over 2} = 36^\circ \cr & \widehat {CMN} + \widehat {NMR} + \widehat {BMR} = 180^\circ \cr & \Rightarrow \widehat {NMR} \cr &= 180^\circ - \left( {\widehat {CMN} + \widehat {BMR}} \right) \cr & = 180^\circ - \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr} \)
∆ ARQ cân tại A
\(\eqalign{ & \Rightarrow \widehat {ARQ} = \widehat {AQR} = {{180^\circ - \widehat A} \over 2} = {{180^\circ - 108^\circ } \over 2} = 36^\circ \cr & \widehat {BRM} + \widehat {MRQ} + \widehat {ARQ} = 180^\circ \cr & \Rightarrow \widehat {MRQ} = 180^\circ - \left( {\widehat {BRM} + \widehat {ARQ}} \right) \cr & = 180^\circ - \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr} \)
∆ QEP cân tại E
\(\eqalign{ & \Rightarrow \widehat {EQP} = \widehat {EPQ} = {{180^\circ - \widehat E} \over 2} = {{180^\circ - 108^\circ } \over 2} = 36^\circ \cr & \widehat {AQR} + \widehat {RQP} + \widehat {EQP} = 180^\circ \cr & \Rightarrow \widehat {RQP} = 180^\circ - \left( {\widehat {AQR} + \widehat {EQP}} \right) \cr & = 180^\circ - \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr & \widehat {EPQ} + \widehat {QPN} + \widehat {DPN} = 180^\circ \cr & \Rightarrow \widehat {QPN} = 180^\circ - \left( {\widehat {EPQ} + \widehat {DPN}} \right) \cr & = 180^\circ - \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr} \)
uy ra : \(\widehat {PNM} = \widehat {NMR} = \widehat {MRQ} = \widehat {RQP} = \widehat {QPN}\)
Vậy MNPQR là ngũ giác đều
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





