Bài 6 trang 81 SGK Toán 8 Chân trời sáng tạo Tập 1
Quan sát Hình 21. Chứng minh rằng tứ giác EFGH là hình thoi?
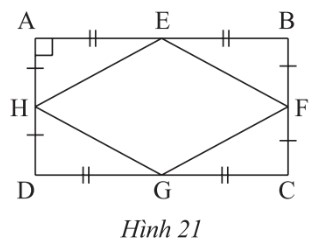
Hướng dẫn giải chi tiết Bài 6
Ta có: \(AE = EB\) nên \(AB = 2AE\).
\(DG = GC\) nên \(DC = 2DG\).
Mà \(AE = DG\) nên \(AB = DC\).
Chứng minh tương tự ta cũng có: \(AD = BC\).
Tứ giác \(ABCD\) có \(AB = DC\) và \(AD = BC\) nên là hình bình hành (dấu hiệu nhận biết).
Suy ra \(AB // CD\) và \(AD // BC\).
Lại có AD ⊥ AB nên AD ⊥ CD; AB ⊥ BC; BC ⊥ CD.
Xét\( \Delta{AEH}\) và \( \Delta{BEF}\) có:
; \(AE = BE; AH = BF\).
Do đó \( \Delta{AEH} = \Delta{BEF}\) (hai cạnh góc vuông).
Suy ra \(HE = FE\) (hai cạnh tương ứng).
Chứng minh tương tự ta cũng có: \(HE = HG; HE = FG\).
Do đó \(HE = EF = FG = GH\).
Tứ giác \(EFGH\) có \(HE = EF = FG = GH\) nên là hình thoi.
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài 4 trang 80 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 5 trang 80 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 7 trang 81 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 8 trang 81 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 9 trang 81 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT





