Bài tập 4 trang 51 SBT Toán 11 Tập 2 Chân trời sáng tạo
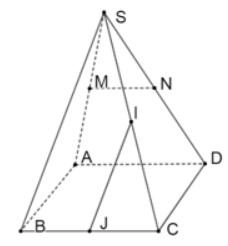
Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N, I, J lần lượt là trung điểm của SA, SD, SC và BC. Tính góc giữa các cặp đường thẳng sau:
a) IJ và DC;
b) MN và IJ.
Hướng dẫn giải chi tiết Bài tập 4
a) Ta có: \(\left\{ \begin{matrix} IJ//SB \\ CD//AB \\ \end{matrix} \right.\)
.
Từ giả thiết, ta có ∆SAB là tam giác đều.
.
b)Ta có: \(\left\{ \begin{matrix} IJ//SB \\ MN//AD//BC \\ \end{matrix} \right.\)
.
Từ giả thiết, ta có ∆SBC là tam giác đều.
Do đó .
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





