Hãy cùng khám phá bài học thú vị Bài 5: Đánh giá thuật toán. Trong bài này, các em sẽ trình bày được sơ lược khái niệm độ phức tạp thời gian của thuật toán. Nêu được ví dụ minh hoạ và biết được kí pháp O lớn và các bậc độ phức tạp thời gian. HOC247 mong rằng sẽ mang đến cho các em những kiến thức bổ ích qua các bài học của chương trình Tin học 11 Khoa học máy tính. Chúc các em học tốt và tích lũy được những kiến thức cần thiết để vươn tới thành công.
Tóm tắt lý thuyết
1.1. Các khái niệm cơ bản
- Đánh giá thuật toán trong Tin học dựa trên tính hiệu quả.
- Thuật toán hiệu quả là khi thời gian thực hiện và lượng bộ nhớ cần dùng ít hơn.
- Tính ngắn gọn, dễ hiểu và dễ lập trình không phải là tiêu chuẩn quan trọng nhất.
Ước lượng thời gian thực thi chương trình và hiệu quả thời gian của thuật toán
- Python có lệnh time() để bẩm giờ tính thời gian thực thi chương trình. Tuy nhiên, cách tính này không áp dụng được để so sánh hiệu quả thuật toán vì những vấn đề sau:
+ Phải lập trình và chạy thử các thuật toán cần so sánh.
+ Thời gian đo được phụ thuộc vào nhiều yếu tố không liên quan tới thuật toán.
+ Không khả thi để tính thời gian trung bình cho nhiều chương trình khác nhau.
Kích thước đầu vào
- Thời gian chạy chương trình phụ thuộc vào kích thước dữ liệu đầu vào (đại diện bằng số tự nhiên n).
- Kích thước dữ liệu đầu vào ảnh hưởng đến thời gian chạy của chương trình.
- Ví dụ, trong bài toán tìm kiếm số hay sắp xếp dãy số, kích thước đầu vào n là độ dài của dãy số.
1.2. Độ phức tạp thời gian của thuật toán
- Thời gian chạy chương trình với đầu vào kích thước n là hàm số T(n) của n.
- Độ phức tạp thời gian ước lượng thời gian thực hiện thuật toán dựa trên số phép toán cần thiết để thực hiện thuật toán với kích thước đầu vào n.
- Tuy nhiên, tính toán số phép toán này không dễ dàng vì khó xác định tương ứng số các phép toán bit với mỗi phép toán và các phép toán số học cũng có thể đếm là nhiều phép toán.
- Trong phân tích thuật toán, phân biệt phép toán sơ cấp và phần còn lại không sơ cấp.
- Một phép toán sơ cấp có thời gian thực hiện không phụ thuộc vào kích thước đầu vào.
- Các phép toán số học, phép so sánh và các hàm toán học với đầu vào giá trị cụ thể được xem là phép toán sơ cấp.
- Phép lặp và phép lựa chọn không phải là phép toán sơ cấp.
1.3. Ví dụ về độ phức tạp thời gian hằng số và độ phức tạp thời gian tuyến tính
Độ phức tạp thời gian hằng số
- Thuật toán có độ phức tạp thời gian hằng số không phụ thuộc vào kích thước đầu vào.
- Ví dụ, thuật toán tính tổng với chỉ 3 phép toán là một thuật toán hằng số.
- Nhà toán học Friedrich Gauss đã đưa ra cách giải này khi còn là học sinh phổ thông.
Độ phức tạp thời gian tuyến tính
- Thuật toán có độ phức tạp thời gian tuyến tính khi số phép toán cần thực hiện là hàm tuyến tính của kích thước đầu vào n.
- Ví dụ, cách giải đầu tiên trong hoạt động trên là một thuật toán tuyến tính vì số phép toán cần thực hiện là T(n) = n - 1.
1.4. Kí pháp và các bậc độ phức tạp thời gian
Cách ước lượng làm già thêm
- Số phép toán cần thiết để thực hiện thuật toán phụ thuộc vào trường hợp dễ hoặc khó của bài toán, không chỉ phụ thuộc vào kích thước đầu vào.
- Ví dụ, trong thuật toán tìm số lớn nhất trong dãy số, số phép toán cần thiết phụ thuộc vào dãy số đầu vào. Nếu dãy số ban đầu là tăng chặt, thì số phép toán cần thiết là nhiều nhất. Nếu phần tử đầu tiên của dãy là số lớn nhất, thì số phép toán cần thiết là ít nhất.
- Có thể xét ba trường hợp trong việc đánh giá độ phức tạp của thuật toán: trường hợp thuận lợi nhất, trường hợp bất lợi nhất và trường hợp ngẫu nhiên.
- Tuy nhiên, để đưa ra ước lượng trung bình, không dễ tìm ra phương pháp chính xác. Thay vào đó, người ta thường sử dụng cách ước lượng làm già thêm để đảm bảo rằng trong thực tế, không có trường hợp nào vượt quá ước lượng đã đưa ra.
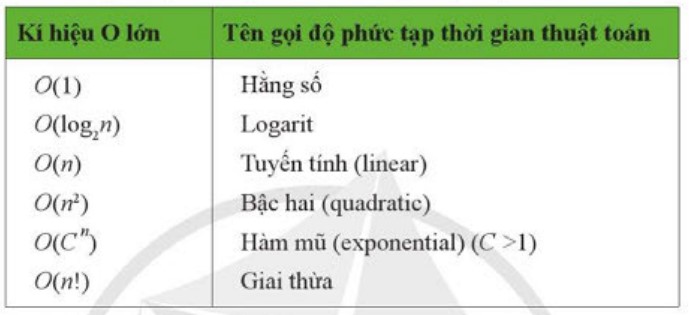
Kí pháp O lớn
- Thuật toán có độ phức tạp thời gian là hằng số nếu số phép toán sơ cấp cần thực hiện không phụ thuộc vào n và không vượt quá một hằng số C. Kí hiệu T(n) = O(1).
- Thuật toán có độ phức tạp thời gian là tuyến tính nếu số phép toán sơ cấp cần thực hiện không vượt quá một hàm tuyến tính của n. Kí hiệu T(n) = O(n).
- Bảng 1 dưới đây là một số kí hiệu O lớn về thời gian thực hiện thuật toán thường gặp:
- Một số công thức liên quan:
+ Công thức 1: Nếu \(f_{1}(n)= O(g_{1}(n))\) và \(f_{2}(n) = O(g_{2}(n))\) thì \(f_{1}(n) + f_{2}(n)= O(max(g_{1}(n), g_{2}(n)))\). Công thức áp dụng cho hai cấu trúc điều khiển được thực hiện tuần tự.
+ Công thức 2: Nếu \(f_{1}(n)= O(g_{1}(n))\) và \(f_{2}(n) = O(g_{2}(n))\) thì \(f_{1}(n) x f_{2}(n)= O(g_{1}(n) x g_{2}(n))\). Công thức áp dụng cho hai cấu trúc điều khiển lồng nhau.
1.5. Các quy tắc khi ước lượng thời gian thực hiện thuật toán
Quy tắc chung
- Các quy tắc ước lượng cho phép bỏ bớt những phần có bậc thấp hơn và chỉ giữ lại những phần có bậc cao nhất và hằng số nhân C đều coi là 1.
- Mô tả thuật toán sử dụng ba cấu trúc: tuần tự, rẽ nhánh, lặp. Cấu trúc tuần tự gồm phép toán sơ cấp và không sơ cấp. Cấu trúc rẽ nhánh và lặp có thể chứa các dãy phép toán tuần tự. Cần ước lượng số phép toán từ bên trong trở ra ngoài.
Lời gọi hàm
- Hàm trong chương trình là một chương trình con, thực hiện một thuật toán cụ thể.
- Đối với lời gọi hàm với đầu vào là giá trị cụ thể không phụ thuộc n, độ phức tạp thời gian là \(T(n)=O(1)\).
- Đối với các trường hợp khác, độ phức tạp thời gian được ước lượng như một thuật toán.
Cấu trúc tuần tự và quy tắc lấy max
- Cấu trúc tuần tự: dãy gồm C phép toán; C là số xác định, không phụ thuộc n.
- Nếu tất cả C phép toán là sơ cấp, độ phức tạp thời gian là \(T(n) = O(1)\).
- Ngược lại, thời gian thực hiện bằng ước lượng lớn nhất trong số các ước lượng của các phép toán trong dãy.
Cấu trúc rẽ nhánh và quy tắc lấy max
- Máy tính thực thi cấu trúc rẽ nhánh (hai nhánh hoặc nhiều nhánh) kiểm tra điều kiện và thực hiện một trong các nhánh.
- Kiểm tra điều kiện là tính giá trị biểu thức logic (bao gồm biểu thức số học và phép so sánh), độ phức tạp thời gian là \(T(n) = O(1)\).
- Độ phức tạp thời gian của cấu trúc rẽ nhánh là độ phức tạp lớn nhất trong các độ phức tạp của các nhánh.
- Độ phức tạp thời gian của việc kiểm tra điều kiện trong cấu trúc rẽ nhánh có thể không còn là \(O(1)\).

Hình 1. Mã giả và độ phức tạp thời gian để tính tổng dãy số
- Nếu như chưa biết trước, việc kiểm tra dãy có phải là cấp số cộng hay không sẽ cần thời gian \(O(n)\).
- Độ phức tạp thời gian của cấu trúc rẽ nhánh trong Hình 1 là \(O(n)\) trong mọi trường hợp.
Cấu trúc vòng lặp và quy tắc nhân
- Máy tính thực hiện cấu trúc vòng lặp sẽ kiểm tra điều kiện và thực hiện thân vòng lặp (bao gồm các phép toán tuần tự, phép lựa chọn hay phép lặp khác).
- Thời gian thực hiện cấu trúc vòng lặp tính bằng số lần lặp nhân với tổng thời gian kiểm tra điều kiện lặp và thời gian thực hiện thân vòng lặp.
- Ví dụ: độ phức tạp thời gian của thuật toán tìm giá trị cực tiểu một dãy số \(a_{1}, a_{2}, a_{3},..., a_{n}\) là \(O(n)\).

Mã giả và số phép toán sơ cấp để tìm cực tiểu của một dãy số
Bài tập minh họa
Tại sao không thể đánh giá thuật toán qua chương trình cài đặt thuật toán?
Hướng dẫn giải:
- Không thể đánh giá thuật toán chỉ dựa trên chương trình cài đặt thuật toán vì việc đánh giá thuật toán yêu cầu xem xét các khía cạnh khác nhau của thuật toán, chứ không chỉ là chương trình cài đặt của nó.
- Chương trình cài đặt thuật toán chỉ là một trong những bước để triển khai thuật toán, nhưng để đánh giá thuật toán, chúng ta cần xem xét các khía cạnh khác nhau như hiệu suất, tốc độ, độ chính xác, bộ nhớ cần thiết, độ phức tạp tính toán, và tính ổn định của thuật toán khi được áp dụng trong các trường hợp khác nhau.
Vì vậy, để đánh giá hiệu quả của một thuật toán, chúng ta cần thực hiện các thí nghiệm và kiểm tra kết quả của thuật toán trên các bộ dữ liệu khác nhau, thay vì chỉ dựa trên chương trình cài đặt của nó. Các thí nghiệm này thường được thiết kế để đánh giá khả năng của thuật toán xử lý các tình huống khác nhau và đo lường các chỉ số hiệu suất khác nhau.
3. Luyện tập Bài 5 Chủ đề FCS SGK Tin học 11 Cánh diều
Học xong bài này, em sẽ:
- Trình bày được sơ lược khái niệm độ phức tạp thời gian của thuật toán. Nêu được ví dụ minh hoạ.
- Biết được kí pháp O lớn và các bậc độ phức tạp thời gian.
3.1. Trắc nghiệm Bài 5 Chủ đề FCS SGK Tin học 11 Cánh diều
Như vậy là các em đã xem qua bài giảng Bài 5 Chủ đề FCS SGK Tin học 11 Cánh diều Khoa học máy tính. Để củng cố kiến thức bài học mời các em tham gia bài tập trắc nghiệm Trắc nghiệm Tin học 11 Cánh diều Chủ đề FCS Bài 5.
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập Bài 5 Chủ đề FCS SGK Tin học 11 Cánh diều
Các em có thể xem thêm phần hướng dẫn Giải bài tập Tin học 11 Cánh diều Chủ đề FCS Bài 5 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Khởi động trang 107 SGK Tin học 11 Cánh diều - CD
Hoạt động trang 108 SGK Tin học 11 Cánh diều - CD
Luyện tập trang 112 SGK Tin học 11 Cánh diều - CD
Vận dụng 1 trang 112 SGK Tin học 11 Cánh diều - CD
Vận dụng 2 trang 112 SGK Tin học 11 Cánh diều - CD
Câu hỏi 1 trang 112 SGK Tin học 11 Cánh diều - CD
Câu hỏi 2 trang 112 SGK Tin học 11 Cánh diều - CD
Câu hỏi 3 trang 112 SGK Tin học 11 Cánh diều - CD
4. Hỏi đáp Bài 5 Chủ đề FCS SGK Tin học 11 Cánh diều
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Tin học của HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Tin Học 11 HỌC247













