-
Câu hỏi:
Một ngọn đèn nhỏ \(S\) đặt ở đáy một bể nước \(\left( {n = \frac{4}{3}} \right)\), độ cao mực nước \(h = 60\,\,\left( {cm} \right)\). Bán kính \(r\) bé nhất của tấm gỗ tròn nổi trên mặt nước sao cho không một tia sáng nào từ \(S\) lọt ra ngoài không khí là:
- A. \(r = 49\,\,\left( {cm} \right)\).
- B. \(r = 53\,\,\left( {cm} \right)\).
- C. \(r = 68\,\,\left( {cm} \right)\).
- D. \(r = 51\,\,\left( {cm} \right)\).
Lời giải tham khảo:
Đáp án đúng: C
Để không có tia sáng ra ngoài không khí, tia sáng bị phản xạ toàn phần tại mặt phân cách
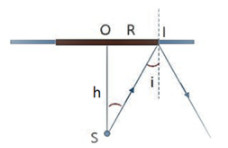
Để xảy ra hiện tượng phản xạ toàn phần, ta có:
\(\sin i \ge \sin {i_{gh}} \Rightarrow \sin i \ge \frac{1}{n}\)
Lại có: \(\sin i = \frac{r}{{\sqrt {{r^2} + {h^2}} }} = \frac{1}{{\sqrt {1 + \frac{{{h^2}}}{{{r^2}}}} }}\)
\(\begin{array}{l} \Rightarrow \frac{1}{{\sqrt {1 + \frac{{{h^2}}}{{{r^2}}}} }} \ge \frac{1}{n} \Rightarrow \sqrt {1 + \frac{{{h^2}}}{{{r^2}}}} \le n\\ \Rightarrow 1 + \frac{{{h^2}}}{{{r^2}}} \le {n^2} \Rightarrow \frac{{{h^2}}}{{{r^2}}} \le {n^2} - 1\\ \Rightarrow \frac{h}{r} \le \sqrt {{n^2} - 1} \Rightarrow r \ge \frac{h}{{\sqrt {{n^2} - 1} }} \\\Rightarrow {r_{\min }} = \frac{h}{{\sqrt {{n^2} - 1} }} = \frac{{60}}{{\sqrt {{{\left( {\frac{4}{3}} \right)}^2} - 1} }} \approx 68\,\,\left( {cm} \right)\end{array}\)
Chọn C.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Chiều của lực Lorenxơ phụ thuộc vào:
- Phát biểu nào sau đây không đúng? A. Lực tương tác giữa hai dòng điện đặt song song có phương nằm trong mặt phẳng hai dòng điện và vuông góc với hai dòng điện
- Một electron bay vào không gian có từ trường đều \(\overrightarrow B \) với vận tốc ban đầu \(\overrightarrow {{v_o}} \) vuông góc với cảm ứng từ. Quỹ đạo của electron trong từ trường là một đường tròn có bán kính R. Khi tăng độ lớn của cảm ứng từ lên gấp đôi thì:
- Nguyên nhân gây ra suất điện động cảm ứng trong thanh dây dẫn chuyển động trong từ trường là:
- Chọn phát biểu sai A. Một tấm kim loại dao động giữa hai cực của một nam châm thì trong tấm kim loại xuất hiện dòng điện Fu-cô
- Một dây dẫn thẳng dài có dòng điện I chạy qua. Hai điểm M và N nằm trong cùng một mặt phẳng chứa dây dẫn, đối xứng với nhau qua dây. Kết luận nào sau đây là không đúng?
- Đặc tính chung của dòng điện Fu-cô là:
- Lực từ tác dụng lên một đoạn dây dẫn mang dòng điện được xác định bởi biểu thức:
- Cho mạch điện như hình vẽ sau Hiện tượng tự cảm phát sinh khi mạch điện có hiện tượng nào sau đây:
- Hai dây dẫn thẳng song song mang dòng điện I1 và I2 đặt cách nhau một khoảng r trong không khí. Trên mỗi đơn vị dài của mỗi dây chịu tác dụng của lực từ có độ lớn là:
- Khung dây dẫn ABCD được đặt trong từ trường đều như hình vẽ Coi rằng bên ngoài vùng MNPQ không có từ trường. Khung chuyển động dọc theo hai đường xx’, yy’. Trong khung sẽ xuất hiện dòng điện cảm ứng khi:
- Tương tác nào sau đây không phải là tương tác từ?
- Phát biểu nào sau đây là sai khi nói về từ phổ?
- Dựa vào hiện tượng nào người ta xác định phương của cảm ứng từ?
- Đơn vị nào sau đây cũng được coi là đơn vị của cảm ứng từ B?
- Một đoạn dây dẫn thẳng dài 1 m mang dòng điện 10 A, đặt trong một từ trường có cảm ứng từ bằng 0,1 T thì chịu một lực 1 N. Góc lệch giữa đường sức từ và dòng điện trong dây dẫn là:
- Cảm ứng từ tại điểm M nằm trên đường sức từ của dòng điện thẳng, bán kính R có giá trị B. Tại điểm M’ trên đường sức từ có bán kính R’ = 3R thì cảm ứng từ có giá trị là:
- Đặc điểm nào sau đây không phải là đặc điểm của từ trường của dòng điện tròn?
- Nếu tăng chiều dài và số vòng của ống dây lên cùng hai lần thì độ lớn cảm ứng từ trong lòng ống dây sẽ
- Trong công thức tính lực Lo-ren-xơ: \(f\, = \,\left| q \right|vB\sin \,\alpha ,\,\alpha \) là
- Hai dây dẫn thẳng, dài có hai dòng điện chiều chạy qua. Chọn phát biểu đúng.
- Một hạt mang điện tích 3,2.10-19 C bay vào trong từ trường đều có cảm ứng từ B = 0,5T, theo hướng hợp với hướng của từ trường một góc 300. Lực Lo-ren-xơ tác dụng lên hạt có độ lớn 8.10-14 N. Vận tốc của hạt khi bắt đầu chuyển động trong từ trường là:
- Một prôtôn chuyển động theo quỹ đạo tròn bán kính 5 cm trong một từ trường đều có B = 0,2 T. Biết mp = 1,672.10-27 kg; diện tích prôtôn q = 1,6.10-19 C. Vận tốc chuyển động của prôtôn là:
- Chọn câu sai.Động cơ điện 1 chiều
- Cuộn dây dẫn tròn bán kính 5 cm gồm 100 vòng dây quấn sát nhau, mỗi vòng dây có dòng điện I = 0,4 A chạy qua. Cảm ứng từ ở tâm vòng dây có độ lớn là:
- Vật liệu nào sau đây không thể làm nam châm?
- Một đoạn dây điện nằm song song với các đường sức từ, cùng chiều với đường sức từ. Lực từ \(\overrightarrow F \) tác dụng lên đoạn dây điện có giá trị là;
- Chiếu một chùm tia sáng đỏ hẹp coi như một tia sáng mặt bên của một lăng kính có tiết diện thẳng là tam giác câ
- Một khung dây phẳng có diện tích \(10\,\,c{m^2}\) đặt trong trường đều, mặt phẳng khung dây hợp với đường cảm �
- Đơn vị từ thông là gì?
- Phát biểu nào sau đây không đúng về phản xạ?
- Một khung tròn bán kính \(R = 4\,\,cm\) gồm \(10\) vòng dây.
- Hai dòng điện cùng chiều cường độ \({I_1} = {I_2} = 10\,\,A\) chạy trong hai dây dẫn thẳng song song dài vô hạn, được đặt trong chân không cách nhau một khoảng \(a = 10\,\,cm\). Một điểm \(M\) cách đều hai dòng điện một khoảng \(x\). Để cảm ứng từ tổng hợp tại \(M\) đạt giá trị lớn nhất thì \(x\) có giá trị là bao nhiêu? Giá trị cảm ứng từ cực đại \({B_{max}}\) khi đó là bao nhiêu?
- Một ngọn đèn nhỏ \(S\) đặt ở đáy một bể nước \(\left( {n = \frac{4}{3}} \right)\), độ cao mực nước \(h = 60\,\,\left( {cm} \right)\). Bán kính \(r\) bé nhất của tấm gỗ tròn nổi trên mặt nước sao cho không một tia sáng nào từ \(S\) lọt ra ngoài không khí là:
- Đường sức từ dòng điện gây ra bởi
- Năng lượng từ trường ống dây có dạng biểu thức là:
- Chiếu một tia sáng đến lăng kính thì thấy tia ló ra là một tia sáng đơn sắc. Có thể kết luận tia sáng chiếu tới lăng kính là ánh sáng:
- Một hạt electron với vận tốc ban đầu bằng \(0\), được gia tốc qua một hiệu điện thế \(400\,\,\left( V \right)\). Tiếp đó, nó được dẫn vào một miền từ trường với véc-tơ cảm ứng từ vuông góc với véc-tơ vận tốc của electron. Quỹ đạo của electron là một đường tròn bán kính \(R = 7\,\,\left( {cm} \right)\). Độ lớn cảm ứng từ là
- Dòng điện trong kim loại là dòng dịch chuyển có hướng của: A. các ion âm, electron tự do ngược chiều điện trường.
- Đơn vị suất điện động là:







