-
Câu hỏi:
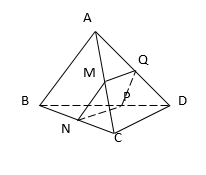
Cho tứ diện \(ABCD\) và \(M\) là điểm ở trên cạnh \(AC\). Mặt phẳng \(\left( \alpha \right)\) qua và \(M\) song song với \(AB\) và \(CD\). Thiết diện của tứ diện cắt bởi \(\left( \alpha \right)\) là
- A. hình bình hành.
- B. hình chữ nhật.
- C. hình thang.
- D. hình thoi.
Lời giải tham khảo:
Đáp án đúng: A
Chọn A.
Trên \(\left( ABC \right)\) kẻ \(MN\text{//}AB;\,\,\,N\in BC\)
Trên \(\left( BCD \right)\) kẻ \(NP\text{//}CD;\,\,\,P\in BD\)
Ta có \(\left( \alpha \right)\) chính là mặt phẳng \(\left( MNP \right)\)
Sử dụng đính lý ba giao tuyến ta có
\(\left( MNP \right)\cap AD=\left\{ Q \right\}\) với \(MQ\text{//}CD\text{//}NP\)
Ta có
\(\left. \begin{align} & MQ\text{//}NP\text{//}CD \\ & MN\text{//}PQ\text{//}AB \\ \end{align} \right\}\) \(\Rightarrow \) thiết diện \(MNPQ\) là hình bình hành.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Trong không gian, số vị trí tương đối giữa đường thẳng và mặt phẳng là?
- Cho tứ diện \(ABCD\). Gọi \(G\) là trọng tâm của tam giác \(ABD\) và \(M\) là điểm trên cạnh \(BC\) sao cho \(BM=2MC\)
- Cho hai đường thẳng \(a\) và \(b\) chéo nhau. Số mặt phẳng chứa \(a\) và song song với \(b\) là bao nhiêu?
- Cho mặt phẳng \(\left( P \right)\) và điểm \(A\) không thuộc mặt phẳng \(\left( P \right)\).
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\), \(I\) là trung điểm cạnh \(SC\). Khẳng định nào sau đây SAI?
- Khẳng định nào sau đây đúng? Đường thẳng \(a\subset mp\left( P \right)\) và
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang, \(AD\text{//}BC\), \(AD=2.BC\), \(M\) là trung điểm \(SA\).
- Cho tứ diện \(ABCD\) và \(M\) là điểm ở trên cạnh \(AC\). Mặt phẳng \(\left( \alpha \right)\) qua và \(M\) song song với \(AB\) và \(CD\).
- Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(d\not\subset \left( \alpha \right)\). Khẳng định nào sau đây sai?
- Cho hai đường thẳng \(a\) và \(b\) cùng song song với \(mp\left( P \right)\). Khẳng định nào sau đây không sai?
