-
Câu hỏi:
Cho hình lăng trụ tam giác \(ABC.{A}'{B}'{C}'\) có các cạnh bên hợp với đáy những góc bằng \(60{}^\circ \), đáy \(ABC\) là tam giác đều và \({A}'\) cách đều \(A\), \(B\), \(C\). Tính khoảng cách giữa hai đáy của hình lăng trụ.
- A. \(a\).
- B. \(a\sqrt{2}\).
- C. \(\frac{a\sqrt{3}}{2}\).
- D. \(\frac{2a}{3}\).
Lời giải tham khảo:
Đáp án đúng: A
Chọn A.
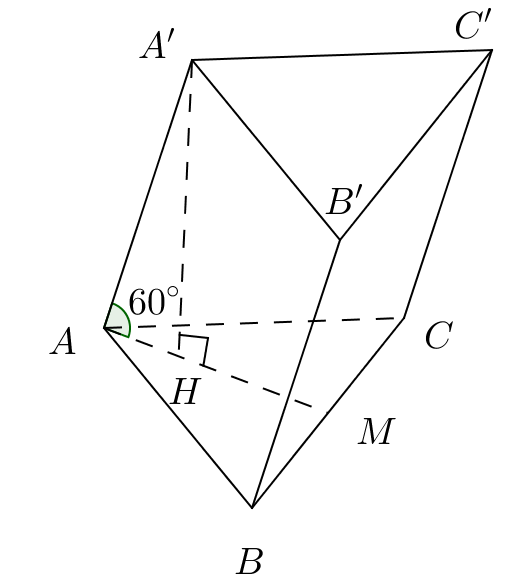
Vì \(\vartriangle ABC\) đều và\(A{A}'={A}'B={A}'C\Rightarrow {A}'ABC\) là hình chóp đều.
Gọi \({A}'H\) là chiều cao của lăng trụ, suy ra H là trọng tâm \(\vartriangle ABC\), \({A}'\overset{\scriptscriptstyle\frown}{A}H=60{}^\circ \).
\({A}'H=AH.\tan 60{}^\circ =\frac{a\sqrt{3}}{3}\sqrt{3}=a\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Trong các mệnh đề sau, mệnh đề nào sai? Nếu hai đường thẳng a và b chéo nhau và vuông góc với nhau thì
- Cho tứ diện đều \(ABCD\) có cạnh bằng \(a\). Khoảng cách giữa hai cạnh đối \(AB\) và \(CD\)
- Trong các mệnh đề sau, mệnh đề nào đúng? Đường vuông góc chung của hai đường thẳng chéo nhau
- Cho tứ diện đều \(ABCD\) có cạnh bằng \(a\). Khoảng cách từ \(A\)đến \(\left( BCD \right)\)
- Cho hình lăng trụ tam giác \(ABC.{A}'{B}'{C}'\) có các cạnh bên hợp với đáy những góc
- Cho các khẳng định sau: (1) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất
- Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\)có cạnh bằng \(1\) (đvdt).
- Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) có cạnh bằng \(a\). Khoảng cách giữa \(BB'\) và \(AC\)
- Cho hình chóp \(S.ABCD\) có \(SA\bot \left( ABCD \right)\), đáy \(ABCD\) là hình chữ nhật
- Cho hình chóp \(S.ABCD\) có \(SA\bot \left( ABCD \right)\), đáy \(ABCD\) là hình thang vuông







