-
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và \(SC = a\sqrt 2 \). Gọi H là trung điểm của AB. Hình chiếu vuông góc của điểm S trên mặt phẳng (ABCD) là điểm?
- A. A
- B. B
- C. C
- D. H
Lời giải tham khảo:
Đáp án đúng: D
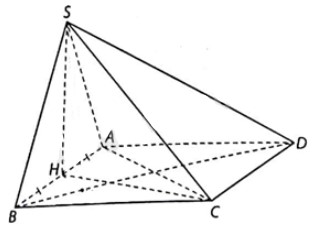
Vì tam giác ABS đều nên SH là đường trung tuyến đồng thời là đường cao.
Áp dụng định lí Pythagore vào tam giác SHB vuông tại H có:
\(SH = \sqrt {S{B^2} - H{B^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
Áp dụng định lí Pythagore vào tam giác CHB vuông tại B có:
\(CH = \sqrt {B{C^2} + H{B^2}} = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}\)
Ta có: \(S{H^2} + H{C^2} = S{C^2}\left( {do\;{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 5 }}{2}} \right)}^2} = {{\left( {a\sqrt 2 } \right)}^2}} \right)\) nên tam giác SHC vuông tại H.
Suy ra: \(SH \bot HC\)
Lại có: \(SH \bot AB\), HC và AB cắt nhau tại H và nằm trong mặt phẳng (ABCD).
Do đó, \(SH \bot \left( {ABCD} \right)\). Vậy H là hình chiếu vuông góc của S trên mặt phẳng (ABCD).
Đáp án D.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Đồ thị hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) luôn?
- Giả sử cường độ ánh sáng I dưới mặt biển giảm dần theo độ sâu theo công thức \(I = {I_o}{a^d}\), trong đó \({I_o}\) là cường độ ánh sáng tại mặt nước biển, a là một hằng số dương, d là độ sâu tính từ mặt nước biển (tính bằng mét). Ở một vùng biển cường độ ánh sáng tại độ sâu 1m bằng 90% cường độ ánh sáng tại mặt nước biển. Giá trị của a là?
- Tập nghiệm của bất phương trình \({2^{{x^2} - x}} \le 4.{\left( {\frac{1}{2}} \right)^x}\) là?
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và \(SC = a\sqrt 2 \). Gọi H là trung điểm của AB. Hình chiếu vuông góc của điểm S trên mặt phẳng (ABCD) là điểm?
- Một chiếc cột dựng trên nền sân phẳng. Gọi O là điểm đặt chân cột trên mặt sân và M là điểm trên cột cách chân cột 30cm. Trên mặt sân, người ta lấy hai điểm A và B cách đều O là 40cm (A, B, O không thẳng hàng). Người ta đo độ dài MA và MB đều bằng 50cm. Chọn khẳng định đúng?
- Khi gửi tiết kiệm P (đồng) theo thể thức trả lãi kép định kì với lãi suất mỗi kì là r (r cho dưới dạng số thập phân) thì số tiền A (cả vốn lẫn lãi) nhận được sau t kì gửi là \(A = P{\left( {1 + r} \right)^t}\) (đồng). Thời gian gửi tiết kiệm cần thiết để số tiền ban đầu tăng gấp ba là?
- Trong các mệnh đề dưới, mệnh đề nào đúng?
- Với \(0 < a \ne 1\) thì?
- Chọn đáp án đúng nhất
- Hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) liên tục trên?
- Rút gọn biểu thức \(\frac{{{x^{\frac{4}{3}}}y + x{y^{\frac{4}{3}}}}}{{\sqrt[3]{x} + \sqrt[3]{y}}}\) (với \(x,y > 0\)) được kết quả là?
- Trong Hóa học, độ pH của một dung dịch được tính theo công thức \(pH = - \log \left[ {{H^ + }} \right]\), trong đó \(\left[ {{H^ + }} \right]\) là nồng độ ion hydrogen tính bằng mol/lít. Tính nồng độ pH của dung dịch có nồng độ ion hydrogen bằng 0,001 mol/lít?
- Chọn đáp án đúng. Với \(a,b > 0\) thì?
- Bất phương trình \({\log _{\frac{1}{6}}}\left( {x + 3} \right) + {\log _{\frac{1}{6}}}\left( {x + 2} \right) \ge - 1\) có nghiệm là?
- Cho \(a > 0,m,n \in \mathbb{R}\). Khẳng định nào sau đây là đúng?
- Chọn đáp án đúng. Cho đường thẳng a vuông góc với mặt phẳng (P), đường thẳng b song song với mặt phẳng (P). Góc giữa hai đường thẳng a và b bằng?
- Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Khẳng định nào sau đây là sai?
- Chọn đáp án đúng. Cho số dương a. Khi đó?
- Bất phương trình \({a^x} > b\left( {0 < a \ne 1} \right)\) có tập nghiệm là \(\mathbb{R}\) khi?
- Hàm số nào dưới đây là hàm số mũ cơ số 3?
- Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và tam giác ABC vuông tại B.
- Nếu x và y thỏa mãn \({4^x} = 16\) và \({3^{x + y}} = 729\) thì y bằng?
- Hàm số nào dưới đây không phải là hàm số lôgarit?
- Cho \(u = u\left( x \right)\) và \(v = v\left( x \right)\) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Mệnh đề nào sau đây đúng?
- Cho đồ thị các hàm số \(y = {a^x},y = {b^x},y = {\log _c}x\) như hình vẽ: Khẳng định nào dưới đây là đúng?
- Chọn đáp án đúng. Nếu hàm số \(y = f\left( x \right)\) có đạo hàm tại \({x_o}\) thì phương trình tiếp tuyến của đồ thị hàm số tại điểm \(M\left( {{x_o};f\left( {{x_o}} \right)} \right)\) là?
- Cho đường thẳng a vuông góc với mặt phẳng (P), đường thẳng b vuông góc với đường thẳng a. Phát biểu nào sau đây là đúng?
- Tập nghiệm của bất phương trình \({\left( {\sqrt 5 } \right)^x} > 5\) là?
- Cho hàm số \(y = f\left( x \right) = {\log _{\sqrt 3 }}x\). Biết rằng: \(\mathop {\max }\limits_{x \in \left[ {3;9} \right]} y = M,\mathop {\min }\limits_{x \in \left[ {3;9} \right]} y = m\). Khi đó?
- Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại A, \(SA \bot \left( {ABC} \right)\). Hình chiếu vuông góc của đường thẳng SC lên mặt phẳng (SAB) là đường thẳng?
- Cho hàm số \(f\left( x \right) = {x^3} + 2{x^2} + 1\) có đồ thị là (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ \(x = 1\) là?
- Cho hình chóp S. ABCD có ABCD là hình chữ nhật và I là 1 điểm thuộc cạnh AB sao cho \(SI \bot AB\). Khi đó, góc giữa hai đường thẳng CD và SI bằng bao nhiêu độ?
- Chọn khẳng định đúng nhất
- Chọn đáp án đúng (Các biểu thức trên đều có nghĩa)?
- Phương trình \({\log _{\frac{1}{2}}}x = - 2\) có nghiệm là?
- Cho hình chóp S. ABCD có tất cả các cạnh đều bằng nhau. Khi đó, góc giữa hai đường thẳng SA và DC bằng?
- Cho hình hộp ABCD.A’B’C’D có \(AA' \bot \left( {ABCD} \right)\). Khẳng định nào dưới đây đúng?
- Chọn đáp án đúng?
- Cho hàm số \(y = f\left( x \right)\) có \(\mathop {\lim }\limits_{x \to - 2} \frac{{f\left( x \right) - f\left( { - 2} \right)}}{{x + 2}} = 5\). Khi đó, \(f'\left( { - 2} \right)\) bằng?
- Góc giữa hai đường thẳng không thể bằng?







