-
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Lấy điểm I trên đoạn SO sao cho SI/SO=2/3. BI cắt SD tại M và DI cắt SB tại N. MNBD là hình gì ?
- A. Hình thang.
- B. Hình bình hành.
- C. Hình chữ nhật.
- D. Tứ diện vì MN và BD chéo nhau.
Lời giải tham khảo:
Đáp án đúng: A
Đáp án: A
Giải thích:
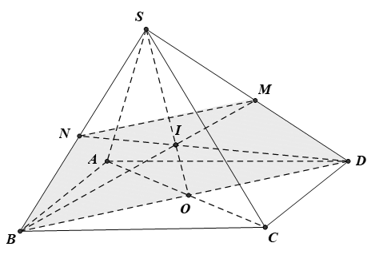
I trên đoạn SO và SI/SO=2/3 nên I là trọng tâm tam giác SBD. Suy ra M là trung điểm SD; N là trung điểm SB
Do đó MN//BD và MN = 1/2 BD nên MNBD là hình thang.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Cho hai đường thẳng song song a và b. Có bao nhiêu mặt phẳng chứa a và song song với b ?
- Cho đường thẳng a nằm trong mp(α) và đường thẳng b⊄(α). Mệnh đề nào sau đây đúng?
- Cho hai đường thẳng a và b cùng song song với mp(P). Khẳng định nào sau đây không sai?
- Khẳng định nào sau đây đúng? Đường thẳng a⊂mp(P) và mp(P)// đường thẳng Δ ⇒ a//Δ.
- Trong không gian có bao nhiêu vị trí tương đối giữa đường thẳng và mặt phẳng?
- Cho hình chóp S.ABCD với đáy ABCD là tứ giác lồi. Thiết diện của mặt phẳng (α) tuỳ ý với hình chóp không thể là:
- Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Lấy điểm I trên đoạn SO sao cho SI/SO=2/3.
- Cho hình chóp tứ giác S.ABCD. Gọi M và N lần lượt là trung điểm của SA và SC. Khẳng định nào sau đây đúng?
- Với điều kiện nào sau đây thì đường thẳng a // với mặt phẳng (∝) ?
- Cho tứ diện ABCD. Gọi M là điểm nằm trong tam giác ABC, (α) là mặt phẳng đi qua M và song song với các đường thẳng AB và CD.







