Hoc247 xin trân trọng gửi đến các em học sinh Đề cương ôn thi học kì 2 môn Toán lớp 8 được biên soạn đầy đủ và chi tiết, tổng hợp lại những kiến thức quan trọng trong quá trình học. Bên cạnh đó còn gợi ý cho các em một số bài tập tự luyện, đề thi học kì 2 có lời giải chi tiết, giúp các em chuẩn bị thật tốt cho kì thi học kì sắp tới.
1.Ôn tập lý thuyết toán lớp 8 học kì 2
1.1 Ôn tập lý thuyết đại số 8 học kì 2
1.1.1 Ôn tập chương phương trình bậc nhất một ẩn
1.1.2 Ôn tập chương bất phương trình bậc nhất một ẩn
1.2 Ôn tập lý thuyết hình học 8 học kì 2
1.2.1 Ôn tập chương tam giác đồng dạng
1.2.2 Ôn tập chương hình lăng trụ đứng hình chóp đều
2. Bài tập ôn thi toán 8 học kì 2
2.1 Bài tập ôn tập phần đại số ( có lời giải chi tiết)
2.2 Bài tập ôn tập phần đại số ( tự luyện)
2.3 Bài tập ôn tập phần hình học ( có lời giải chi tiết)
2.4 Bài tập ôn tập phần hình học ( tự luyện)
3.1 Đề thi học kì 2 toán 8( Đề số 1)
Đề cương ôn tập học kì 2
Môn :Toán lớp 8
---------------
1.Ôn tập lý thuyết toán lớp 8 học kì 2
1.1 Ôn tập lý thuyết đại số 8 học kì 2
1.1.1 Ôn tập chương phương trình bậc nhất một ẩn
• Định nghĩa: Phương trình dạng ax + b = 0, với a và b là hai số đã cho và , được gọi là phương trình bậc nhất một ẩn.
• Hai quy tắc biến đổi phương trình.
+Quy tắc chuyển vế.
Trong một phương trình, ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.
+Quy tắc nhân với một số.
– Trong một phương trình, ta có thể nhân cả hai vế với cùng một số khác 0.
– Trong một phương trình, ta có thể chia cả hai vế cho cùng một số khác 0.
• Phương trình tương đương.
Hai phương trình tương đương là hai phương trình có cùng một tập nghiệm.
• Giải phương trình là tìm tất cả các nghiệm hay tập nghiệm của phương trình đó
• Phương trình tích: là phương trình có dạng A(x).B(x).C(x).......=0. Trong đó A(x), B(x), C(x),... là những biểu thức của biến x
Cách giải phương trình tích: xét phương trình tích dạng A(x).B(x) = 0 Ta có
A(x).B(x) = 0 A(x) = 0 hoặc B(x) = 0
• Phương trình chứa ẩn ở mẫu
+Tìm điều kiện xác định của một phương trình: Ta tìm điều kiện cho ẩn để tất cả các mẫu trong phương trình đều khác 0 và gọi đó là điều kiện xác định ( ĐKXĐ) của phương trình
+ Cách giải phương trình chứa ẩn ở mẫu.
Bước 1 : Tìm điều kiện xác định của phương trình.
Bước 2 : Quy đồng mẫu hai vế của phương trình rồi khử mẫu.
Bước 3 : Giải phương trình vừa nhận được.
Bước 4 : Kết luận. Trong các giá trị ẩn vừa tìm được ở bước 3, các giá trị thỏa mãn
ĐKXĐ chính là nghiệm của phương trình đã cho.
• Các bước giải bài toán bằng cách lập phương trình:
Bước 1 : Lập phương trình.
– Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
– Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
– Lập phương trinh biểu thị mối quan hệ giữa các đại lượng.
Bước 2 : Giải phương trình.
Bước 3 : Trả lời : Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.
1.1.2 Ôn tập chương bất phương trình bậc nhất một ẩn
• Định nghĩa: Bất phương trình dạng ax + b < 0 (hoặc ax + b > 0, ax + b 0, ax + b 0) trong đó a và b là hai số đã cho, a 0, được gọi là bất phương trình bậc nhất một ẩn
• Hai quy tắc biến đổi bất phương trình.
+Quy tắc chuyển vế.
Khi chuyển vế một hạng tử của bất phương trình từ vế này sang vế kia ta phải đổi dấu hạng tử đó.
+Quy tắc nhân với một số.
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải :
– Giữ nguyên chiều bất phương trình nếu số đó dương.
– Đổi chiều bất phương trình nếu số đó âm.
• Phương trình chứa dấu giá trị tuyệt đối
+ Nhắc lại về giá trị tuyệt đối
| A| = A khi \(A \ge 0\)
| A| = - A khi A <0
+ Phương trình chứa dấu giá trị tuyệt đối |A| = B
Cách 1:\(|A| = B \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} A \ge 0\\ A = B \end{array} \right.\\ \left\{ \begin{array}{l} A < 0\\ - A = B \end{array} \right. \end{array} \right.\) Cách 2: \(|A| = B \Leftrightarrow \left\{ \begin{array}{l} B \ge 0\\ \left[ \begin{array}{l} A = B\\ A = - B \end{array} \right. \end{array} \right.\)
+ Phương trình chứa dấu giá trị tuyệt đối |A| = |B|
\(|A|\, = \,|B|\, \Leftrightarrow \left[ \begin{array}{l} A = B\\ A = - B \end{array} \right.\)
1.2 Ôn tập lý thuyết hình học 8 học kì 2
1.2.1 Ôn tập chương tam giác đồng dạng
• Định lý Ta – lét trong tam giác.
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
• Định lý Ta – lét đảo.
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
• Hệ quả của định lý Ta – let.
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
• Tính chất đường phân giác trong tam giác.
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của đoạn ấy.
• Tam giác đồng dạng.
+ Định nghĩa Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu :
\(\widehat {A} = \widehat A ; \widehat {B } = \widehat B ; \widehat {C} = \widehat C \)
+Định lí: Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
• Ba trường hợp đồng dạng của tam giác.
+Trường hợp thứ nhất (c.c.c)
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
+Trường hợp thứ hai (c.g.c)
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đồng dạng với nhau.
+Trường hợp thứ ba (g.g.g)
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
• Các trường hợp đồng dạng của tam giác vuông.
Hai tam giác vuông đồng dạng với nhau nếu :
– Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia.
– Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.
– Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyện và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
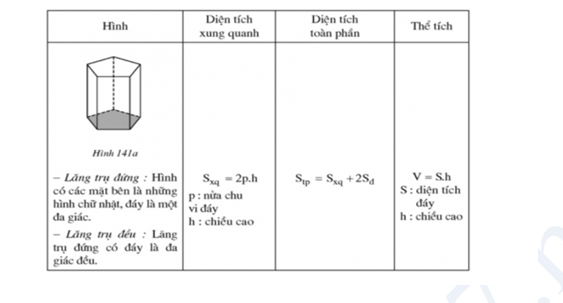
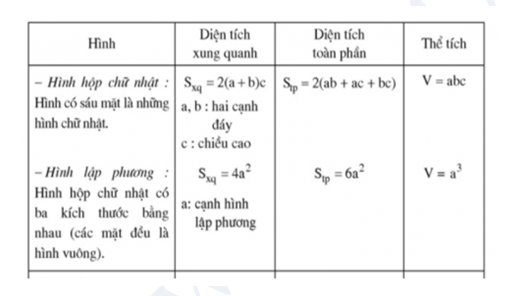
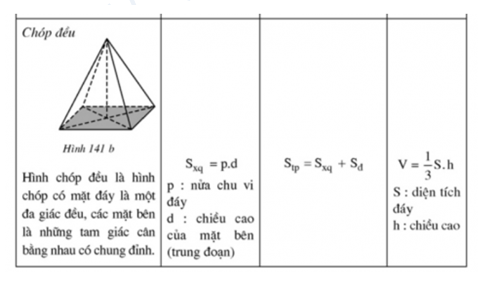
1.2.2 Ôn tập chương hình lăng trụ đứng hình chóp đều
2. Bài tập ôn thi toán 8 học kì 2
2.1 Bài tập ôn tập phần đại số ( có lời giải chi tiết)
1. Giải phương trình
\(a)\;7x{\rm{ }} + {\rm{ }}12{\rm{ }} = {\rm{ }}0\;\;\;\;\;b){\rm{ }}5x{\rm{ }}--{\rm{ }}2{\rm{ }} = {\rm{ }}0\;\;\;\;\;\;\;c){\rm{ }}12{\rm{ }}--{\rm{ }}6x{\rm{ }} = {\rm{ }}0\;\;\;\,\,\,\;d){\rm{ }}--{\rm{ }}2x{\rm{ }} + {\rm{ }}14{\rm{ }} = {\rm{ }}0\)
Giải
\(a. 7x{\rm{ }} + {\rm{ }}12{\rm{ }} = {\rm{ }}0 \Leftrightarrow 7x = - 12 \Leftrightarrow x = - \frac{{12}}{7}\)
Vậy nghiệm của phương trình là \(x = - \frac{{12}}{7}\)
\(b)\,\,\,{\rm{ }}5x{\rm{ }}--{\rm{ }}2{\rm{ }} = {\rm{ }}0\;\; \Leftrightarrow 5x = 2 \Leftrightarrow x = \frac{2}{5}\)
Vậy nghiệm của phương trình là \(x = - \frac{2}{5}\)
\(c){\rm{ }}12{\rm{ }}--{\rm{ }}6x{\rm{ }} = {\rm{ }}0 \Leftrightarrow - 6x = - 12 \Leftrightarrow x = 2\)
Vậy nghiệm của phương trình là x = 2
\(d){\rm{ }}--{\rm{ }}2x{\rm{ }} + {\rm{ }}14{\rm{ }} = {\rm{ }}0 \Leftrightarrow - 2x = - 14 \Leftrightarrow x = 7\)
Vậy nghiệm của phương trình là x = 7
2. Giải phương trình
\(\begin{array}{l} a)\;3x{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}7x{\rm{ }}--{\rm{ }}11\;\,\,\,\,\,\,\,\,\,\,\,\,\,\,e)\;5{\rm{ }}--{\rm{ }}3x{\rm{ }} = {\rm{ }}6x{\rm{ }} + {\rm{ }}7\;\;\;\;\;\;\\ \;b){\rm{ }}2x{\rm{ }} + {\rm{ }}x{\rm{ }} + {\rm{ }}12{\rm{ }} = {\rm{ }}0\;\;\;\;\,\,\,\,\,\,\,\,\,f){\rm{ }}11{\rm{ }}--{\rm{ }}2x{\rm{ }} = {\rm{ }}x{\rm{ }}--{\rm{ }}1\;\;\;\;\;\\ c)\;x{\rm{ }}--{\rm{ }}5{\rm{ }} = {\rm{ }}3{\rm{ }}--{\rm{ }}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,g)\;\;15{\rm{ }}--{\rm{ }}8x{\rm{ }} = {\rm{ }}9{\rm{ }}--{\rm{ }}5x\;\;{\rm{ }}\\ d)\;7{\rm{ }}--{\rm{ }}3x{\rm{ }} = {\rm{ }}9{\rm{ }}--{\rm{ }}x\;\;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,h){\rm{ }}3{\rm{ }} + {\rm{ }}2x{\rm{ }} = {\rm{ }}5{\rm{ }} + {\rm{ }}2x\; \end{array}\)
Giải
\(a.\,\,3x{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}7x{\rm{ }}--{\rm{ }}11 \Leftrightarrow - 4x = - 12 \Leftrightarrow x = 3\)
Vậy nghiệm của phương trình là x = 3
\(b.\,\,2x{\rm{ }} + {\rm{ }}x{\rm{ }} + {\rm{ }}12{\rm{ }} = {\rm{ }}0 \Leftrightarrow 3x = - 12 \Leftrightarrow x = - 4\)
Vậy nghiệm của phương trình là x = - 4
\(c.\,\;x{\rm{ }}--{\rm{ }}5{\rm{ }} = {\rm{ }}3{\rm{ }}--{\rm{ }}x \Leftrightarrow 2x = 8 \Leftrightarrow x = 4\)
Vậy nghiệm của phương trình là x = 4
\(d.\,\;7{\rm{ }}--{\rm{ }}3x{\rm{ }} = {\rm{ }}9{\rm{ }}--{\rm{ }}x \Leftrightarrow - 2x = 2 \Leftrightarrow x = - 1\)
Vậy nghiệm của phương trình là x = -1
3. Giải phương trình
\(\begin{array}{l} a.\,\left( {x + 1} \right)\left( {x + 2} \right)\left( {x + 3} \right) = 0\\ b.\left( {x + 1} \right)(2x + 3) = \left( {{x^2} - 1} \right)\\ c.\,{\left( {2x + 1} \right)^2} = {\left( {x + 1} \right)^2}\\ d.\,{x^3} - 5{x^2} + 6x = 0 \end{array}\)
Giải
\(\begin{array}{l} a.\,\left( {x + 1} \right)\left( {x + 2} \right)\left( {x + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x + 1 = 0\\ x + 2 = 0\\ x + 3 = 0 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = - 2\\ x = - 3 \end{array} \right. \end{array}\)
Vậy nghiệm của phương trình là\(S = \left\{ { - 3; - 2; - 1} \right\}\)
\(\begin{array}{l} b.\left( {x + 1} \right)(2x + 3) = \left( {{x^2} - 1} \right)\\ \Leftrightarrow \left( {x + 1} \right)\left( {2x + 3} \right) - \left( {{x^2} - 1} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {2x + 3 - x + 1} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {x + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x + 1 = 0\\ x + 4 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = - 4 \end{array} \right. \end{array}\)
Vậy nghiệm của phương trình là
\(S = \left\{ { - 4; - 1} \right\}\)
\(\begin{array}{l} \\ c.\,{\left( {2x + 1} \right)^2} = {\left( {x + 1} \right)^2}\\ \Leftrightarrow {\left( {2x + 1} \right)^2} - {\left( {x + 1} \right)^2} = 0\\ \Leftrightarrow \left( {2x + 1 + x + 1} \right)\left( {2x + 1 - x - 1} \right) = 0\\ \Leftrightarrow x.\left( {3x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x = 0\\ 3x + 2 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = - \frac{2}{3} \end{array} \right. \end{array}\)
Vậy nghiệm của phương trình là \(S = \left\{ {0; - \frac{2}{3}} \right\}\)
\(\begin{array}{l} d.\,{x^3} - 5{x^2} + 6x = 0\\ \Leftrightarrow x\left( {{x^2} - 5x + 6} \right) = 0\\ \Leftrightarrow x\left( {x - 2} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x - 2 = 0\\ x - 3 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 2\\ x = 3 \end{array} \right. \end{array}\)
Vậy nghiệm của phương trình là \(S = \left\{ {0;2;3} \right\}\)
{--xem đầy đủ nội dung ở phần xem online hoặc tải về--}
2.2 Bài tập ôn tập phần đại số ( tự luyện)
1. Giải các phương trình sau:
a) 3x + 1 = 7x – 11 e) 15 – 8x = 9 – 5x
b) 2x + x + 12 = 0 f) 3 + 2x = 5 + 2x
c) x – 5 = 3 – x d) 7 – 3x = 9 – x g) 0,25x + 1,5 = 0
d) 5 – 3x = 6x + 7 f) 11 – 2x = x – 1 h) 6,36 – 5,2x = 0
2. Giải các phương trình sau:
c) 7 – (2x + 4) = – (x + 4) d) (x – 2)3 + (3x – 1)(3x + 1) = (x + 1)3
e) (x + 1)(2x – 3) = (2x – 1)(x + 5) f) (x – 1)3 – x(x + 1)2 = 5x(2 – x) – 11(x + 2)
g) (x – 1) – (2x – 1) = 9 – x h) (x – 3)(x + 4) – 2(3x – 2) = (x – 4)2
3. Giải các phương trình sau:
\(\begin{array}{l} a.\,\,\frac{{2\left( {3x + 1} \right) + 1}}{4} - 5 = \frac{{2\left( {3x - 1} \right)}}{5} - \frac{{3x + 2}}{{10}}\\ b.\,\,\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\\ c.\,\,x - \frac{3}{{17}}\left( {2x - 1} \right) = \frac{7}{{34}}\left( {1 - 2x} \right) + \frac{{10x - 3}}{2}\\ d.\,\frac{{5\left( {x - 1} \right) + 2}}{6} - \frac{{7x - 1}}{4} = \frac{{2\left( {2x + 1} \right)}}{7} \end{array}\)
4. Giải các phương trình sau:
a) 2x3 + 5x2 – 3x = 0 b) 2x3 + 6x2 = x2 + 3x
c) x2 + (x + 2)(11x – 7) = 4 d) (x – 1)(x2 + 5x – 2) – (x3 – 1) = 0
e) x3 + 1 = x(x + 1) f) x3 + x2 + x + 1 = 0
g) x3 – 3x2 + 3x – 1 = 0 h) x3 – 7x + 6 = 0
i) x6 – x2 = 0 j)x3 – 12 = 13x
5. Cho phương trình (ẩn x): \({x^3}{\rm{ }} + {\rm{ }}a{x^2}--{\rm{ }}4x{\rm{ }}--{\rm{ }}4{\rm{ }} = {\rm{ }}0\)
a) Xác định m để phương trình có một nghiệm x = 1.
b) Với giá trị m vừa tìm được, tìm các nghiệm còn lại của phương trình.
6. Cho phương trình (ẩn x): \({x^3} - \left( {{m^2} - m + 7} \right)x - 3\left( {{m^2} - m - 2} \right) = 0\)
c) Xác định a để phương trình có một nghiệm x = – 2.
d) Với giá trị a vừa tìm được, tìm các nghiệm còn lại của phương trình.
6. Tìm hai số, biết tổng của hai số bằng 65 và hiệu của chúng là 11.
7. Tìm hai số, biết tổng của hai số bằng 75 và số này gấp đôi số kia.
8. Chu vi một miếng đất hình chữ nhật có chu vi bằng 80m. Nếu giảm chiều rộng 3m và tăng chiều dài 8m thì diện tích tăng thêm 32m2. Tính kích thước miếng đất.
9. Hai người đi xe đạp cùng xuất phát một lúc từ A đến B dài 30 km, vận tốc của họ hơn kém nhau 3 km/h nên đến B sớm muộn hơn nhau 3o phút. Tính vận tốc cảu mỗi người
10. Để hoàn thành một công việc, hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì tổ II được điều đi làm công việc khác, tổ I đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ xong công việc đó.
11. Hai lớp 8A và 8B cùng tham gia lao động vệ sinh sân trường thì cong việc hoàn thành sau 1 giờ 20 phút. Nếu mỗi lớp chia nhau làm nửa công việc thì thời gian hoàn tất là 3 giờ. Hỏi nếu mỗi lớp làm một mình thì phải mất bao nhiêu thời gian
12. Ông của Bình hơn Bình 58 tuổi. Nếu cộng tuổi của bố Bình và hai lần tuổi của Bình thì bằng tuổi của ông và tổng số tuổi của cả ba người là 130. Hãy tính tuổi của Bình
2.3 Bài tập ôn tập phần hình học ( có lời giải chi tiết)
1. Cho tam giác ABC có AB = 15cm, AC = 20cm. Trên hai cạnh AB và AC lần
lượt lấy hai điểm D và E sao cho AD = 8cm, AE = 6cm. Chứng minh: \(\angle AED = \angle ABC\)
Giải
Xét \(\Delta AED\) và \(\Delta ABC\) có:
\(\angle A:\,chung \)
\(\left\{ \begin{array}{l} \frac{{AE}}{{AB}} = \frac{6}{{15}} = \frac{2}{5}\\ \frac{{AD}}{{AC}} = \frac{8}{{20}} = \frac{2}{5} \end{array} \right. \Rightarrow \frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}\)
Vậy \(\Delta AED \sim \Delta ABC\) \( \Rightarrow \angle AED = \angle ABC\,\,\left( {dpcm} \right)\)
2. Cho tam giác ABC, trên cạnh AB lấy điểm M kẻ ML song song với AC ( L\(\in BC\) ) và MN song song với BC ( N\( \in AC\) )
a) Chứng minh tam giác AMN đồng dạng với tam giác ABC
b) Nêu tất cả cá cặp tam giác đồng dạng
Giải
a. Ta có MN || BC nên tam giác AMN và tam giác ABC đồng dạng với nhau
b. Các cặp tam giác đồng dạng là
\(\Delta AMN \sim \Delta ABC\) (cmt)
\(\Delta AML \sim \Delta ABC\) (cm tương tự)
\(\Delta AMN \sim \Delta AML\) ( tính chất bắt cầu)
3. Cho tam giác ABC có các góc nhọn. BE, CF là hai đường cao của tam giác ABC. EM và FN là hai đường cao của tam giác AEF. Chứng minh rằng MN || BC
Giải
Ta có: ME || CF ( cùng vuông góc với AB)
Theo định lí Ta- lét trong tam giác AFC ta có:
\(\frac{{AM}}{{AF}} = \frac{{AE}}{{AC}}\)
Tương tự NF || BE, nên \(\frac{{AF}}{{AB}} = \frac{{AN}}{{AE}}\)
Do đó \(\frac{{AM}}{{AF}}.\frac{{AF}}{{AB}} = \frac{{AE.AN}}{{AC.AE}}\) hay \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)
Vậy MN || BC ( theo định lí Ta –lét đảo)
{--xem đầy đủ nội dung ở phần xem online hoặc tải về--}
2.4 Bài tập ôn tập phần hình học ( tự luyện)
1. Cho hình vuông ABCD có độ dài cạnh là a. Gọi M, N lần lượt là trung điểm của AB và BC . Các đường thẳng DN và CM cắt nhau tại I . Chứng minh rằng :
a. Tam giác CIN vuông
b. Tính diện tích tam giác CIN theo a.
c. Tam giác AID cân.
2. 4.Cho tam giác ABC , M là Trung điểm của cạnh BC. Từ 1 điểm E trên cạnh BC ta kẻ Ex//AM. Ex cắt tia CA ở F và tia BA ở G.Chứng minh rằng :FE + EG = 2 AM
3. Cho tam giác ABC vuông tại A, đường phân giác BD. Biết AD = 3 cm, DC = 5cm. Tính độ dài AB, BC
4. Cho tam giác ABC có các đường phân giác AD, BE, CF. Chứng minh rằng \(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = 1\)
5. Cho tam giác ABC với trung tuyến AM. Đường phân giác của góc AMB cắt cạnh AB ở D, đường phân giác của góc AMC cắt AC ở E. Chứng minh rằng DE || BC
6. Từ một điểm D bất kỳ trên cạnh huyền AB của tam giác vuông ABC, kẻ một đường thẳng vuông góc với AB, cắt BC kéo dài tại E và cạnh AC kéo dài tại K. Chứng minh: AD.BD=DK.DE
7. Cho hình bình hành MNPQ. Một đường thẳng đi qua M cắt các đường thẳng NP, PQ, QN theo thứ tự A, B, C. Chứng minh:
a/ AN.BQ không đổi
b/ \(M{C^2} = {\rm{ }}AC.BC\)
8. Cho hình hộp chữ nhật có các cạnh AB, AD, tỉ lệ với 3, 4, 5 và AC = 1cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp
9. Hình chóp cụt của tứ giác đều ABCDA1B1C1D1 có cạnh đáy AB = 8cm, A1B1= 4cm, cạnh bên là cm.
a/ Tính chiều cao thuộc mặt bên của hình chóp
b/ Tính diện tích xung quanhvà diện tích toàn phần của hình chóp
10. Cho hình chóp SABC có mặt đáy và các mặt bên là những tam giác đều cạnh 10cm. Tính diện tích toàn phần và thể tích của hình chóp
3. Đề thi học kì 2 toán 8
3.1 Đề thi học kì 2 toán 8 ( Đề số 1)
Đề thi học kì 2 toán lớp 8 – Đề số 1
Thời gian làm bài 90 phút, không kể thời gian phát đề
Bài 1: Giải các phương trình sau:
a) (x - 3)2 + 2x - 6 = 0
\(\frac{{2x}}{{x + 2}} + \frac{2}{{x - 2}} = \frac{{{x^2} + 4}}{{{x^2} - 4}}\)
Bài 2: Giải bất phương trình
\(a. \frac{x}{2} + \frac{{1 - x}}{3} > 0 \)
\(b. {\left( {x - 9} \right)^2} - x\left( {x + 9} \right) \le 0\)
Bài 3: Một khu vườn hình chữ nhật có chiều dài hơn chiều rộng 12m. Nếu tăng chiều dài 3m và giảm chiều rộng 1,5m thì diện tích khu vườn không thay đổi. Tính chu vi của khu vườn.
Bài 4: Cho tam giác ABC có 3 góc nhọn, hai đường cao BE, CF cắt nhau tại H.
a) CM: .\(AH \bot BC\)
b) Chứng tỏ: AE.AC = AF.AB
c) Chứng minh:\(\Delta AEF \sim \Delta ABC\)
Hướng dẫn giải
Bài 1: Giải các phương trình sau:
a)
\(\begin{array}{l} \;\,\,\,\,\,\,\,{(x\; - \;3)^2}\; + \;2x - \;6 = \;0\\ \Leftrightarrow {\left( {x - 3} \right)^2} + 2\left( {x - 3} \right)\; = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x - 3 = 0\\ x - 1 = 0 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 3\\ x = 1 \end{array} \right.\; \end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {1;3} \right\}\)
\(b. \frac{{2x}}{{x + 2}} + \frac{2}{{x - 2}} = \frac{{{x^2} + 4}}{{{x^2} - 4}}\)
ĐKXĐ: \(x \ne \pm 2\)
\(\begin{array}{l} \frac{{2x}}{{x + 2}} + \frac{2}{{x - 2}} = \frac{{{x^2} + 4}}{{{x^2} - 4}}\\ \Leftrightarrow \frac{{2x\left( {x - 2} \right) + 2\left( {x + 2} \right) - \left( {{x^2} + 4} \right)}}{{{x^2} - 4}} = 0\\ \Leftrightarrow 2{x^2} - 4x + 2x + 4 - {x^2} - 4 = 0\\ \Leftrightarrow {x^2} - 2x = 0\\ \Leftrightarrow x\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x - 2 = 0 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 0\,\,(nhan)\\ x = 2\,\,(loai) \end{array} \right. \end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ 0 \right\}\)
Bài 2: Giải bất phương trình
a)
\(\begin{array}{l} \,\,\,\,\,\,\frac{x}{2} + \frac{{1 - x}}{3} > 0\\ \Leftrightarrow \frac{{3x + 2\left( {1 - x} \right)}}{6} > 0\\ \Leftrightarrow 3x + 2 - 2x > 0\\ \Leftrightarrow x + 2 > 0\\ \Leftrightarrow x > - 2 \end{array}\)
Vậy tập nghiệm của bất phương trình là \(S = \left\{ {x/x > - 2} \right\}\)
b.
\(\begin{array}{l} \,\,\,\,\,{\left( {x - 9} \right)^2} - x\left( {x + 9} \right) \le 0\\ \Leftrightarrow {x^2} - 18x + 81 - {x^2} - 9x \le 0\\ \Leftrightarrow - 27x + 81 \le 0\\ \Leftrightarrow - 27x \le - 81\\ \Leftrightarrow x \ge 3 \end{array}\)
Vậy tập nghiệm của bất phương trình là \(S = \left\{ {x/x \ge 3} \right\}\)
Bài 3:
Gọi chiều dài của khu vườn hình chữ nhật lúc đầu là x (m) ĐK x >12
Chiều rộng của khu vườn lúc đầu là: x -12 (m)
Chiều dài của khu vườn lúc sau là: x+3 (m)
Chiều rộng của khu vườn lúc sau là: x-12 -1,5 = x- 13,5 (m)
Theo đề bài ta có phương trình
\(\begin{array}{l} \,\,\,\,\,x\left( {x - 12} \right) = \left( {x + 3} \right)\left( {x - 13,5} \right)\\ \Leftrightarrow {x^2} - 12x = {x^2} - 13,5x + 3x - 40,5\\ \Leftrightarrow - 1,5x = - 40,5\\ \Leftrightarrow \,\,x = 27 \end{array}\)
Vậy chiều dài của khu vườn là 27m, chiều rộng của khu vườn là 15 m
Chu vi khu vườn là \(\frac{{27 + 15}}{2} = 21(m)\)
Bài 4: Cho tam giác ABC có 3 góc nhọn, hai đường cao BE, CF cắt nhau tại H.
a) CM: \(AH \bot BC\)
b) Chứng tỏ: AE.AC = AF.AB
c) Chứng minh:\(\Delta AEF \sim \Delta ABC\)
3.2 Đề thi học kì 2 toán 8( Đề số 2)
Đề thi học kì 2 toán lớp 8 – Đề số 2
Thời gian làm bài 90 phút, không kể thời gian phát đề
Giải
3.3 Đề thi học kì 2 toán 8 ( Đề số 3)
Đề thi học kì 2 toán lớp 8 – Đề số 3
Thời gian làm bài 90 phút, không kể thời gian phát đề
Hướng dẫn giải
{--xem đầy đủ nội dung ở phần xem online hoặc tải về--}





.PNG?enablejsapi=1)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)


