Trắc nghiệm Toán 6 kết nối tri thức Bài 37: Số đo góc

 

• Câu 1: Mã câu hỏi: 311221

  Cho điểm O thuộc đường thẳng xy, vẽ tia Oa sao cho \(\widehat {yOa} = {30^0}\). Tính số đo \(\widehat {xOa}\)

  • A. 120⁰
  • B. 150⁰
  • C. 90⁰
  • D. 60⁰

• Câu 2: Mã câu hỏi: 311222

  Em hãy chọn phát biểu sai trong các phát biểu sau:

  • A. Góc bẹt là góc có hai cạnh là hai tia đối nhau
  • B.  \(\widehat A\) được gọi là góc tù nếu \(\widehat A>90^0\)
  • C. Nếu tia Ot là tia phân giác của \(\widehat {xOy}\) thì  \(\widehat {xOt} = \widehat {yOt} = \frac{{\widehat {xOy}}}{2}\)
  • D. Tam giác MNP là hình gồm các đoạn thẳng MN, MP và NP. Khi ba điểm M, N, P không thẳng hàng.     

 

• Câu 3: Mã câu hỏi: 311224

  Cho \( \widehat {AOB} = {135^0}\), điểm C nằm trong \(\widehat {AOB} \) biết  \( \widehat {BOC} = {90^0}\) . Gọi OD là tia đối của tia OC. Tính \(\widehat {AOC} \)

  • A. 50⁰
  • B. 30⁰
  • C. 45⁰
  • D. 35⁰

• Câu 4: Mã câu hỏi: 311228

  Cho hình vẽ. Tính số đo góc \(\widehat {yOz}\)

  

  • A. 50^∘
  • B. 60^∘
  • C. 150^∘
  • D. 70^∘

• Câu 5: Mã câu hỏi: 311230

  Biết \(\widehat {xOy};\widehat {yOz}\)​ là hai góc bù nhau và \(\widehat {yOz} = 140^\circ\)∘ . Tính số đo góc \(\widehat {xOy}\)

  • A. 50^∘
  • B. 60^∘
  • C. 40^∘
  • D. 140^∘

• Câu 6: Mã câu hỏi: 311231

  Biết \(\widehat {xOy};\widehat {yOz}\)​ là hai góc phụ nhau và \(\widehat {yOz} = 20^\circ\). Tính số đo góc \(\widehat {xOy}\)

  • A. 50^∘
  • B. 60^∘
  • C. 40^∘
  • D. 70^∘

• Câu 7: Mã câu hỏi: 311232

  Cho \(\widehat {aOc} = 35^\circ ;\,\widehat {bOc} = 130^\circ\) . Biết tia Oa nằm giữa hai tia Ob và Oc. Tính số đo góc \(\widehat {aOb}\)

  • A. 95^∘
  • B. 90^∘
  • C. 85^∘
  • D. 165^∘

• Câu 8: Mã câu hỏi: 311234

  Cho hình vẽ. Biết tia Oy nằm giữa hai tia Oz và Ox. Tính số đo góc \(\widehat {xOz}\)

  

  • A. 10^∘
  • B. 70^∘
  • C. 85^∘
  • D. 140^∘

• Câu 9: Mã câu hỏi: 311235

  Cho \(\widehat {BOC} = 96^\circ\) . A là một điểm nằm trong góc BOC. Biết \(\widehat {BOA} = 40^\circ\). Vẽ tia OD là tia đối của tia OA. Tính số đo góc \(\widehat {COD}\)

  • A. 123^∘
  • B. 125^∘
  • C. 134^∘
  • D. 124^∘

• Câu 10: Mã câu hỏi: 311237

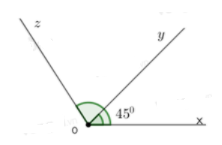
  Tính góc yOz trên hình vẽ sau biết Oy nằm giữa hai tia Ox;Oz và \(\widehat {xOy} = {45^0};\,\widehat {xOz} = {122^0}\)

  

  • A. 66⁰
  • B. 77⁰
  • C. 45⁰
  • D. 100⁰

Đề thi nổi bật tuần