Bài tập 6 trang 71 SGK Toán 8 Chân trời sáng tạo Tập 2
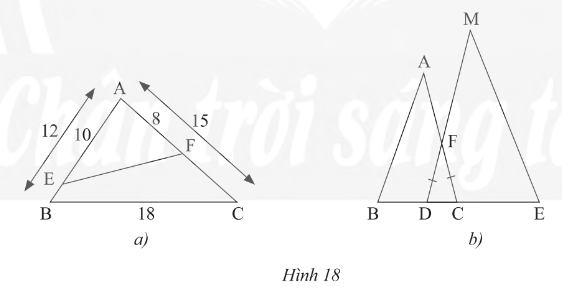
a) Cho tam giác ABC có AB = 12 cm, AC = 15 cm, BC = 18 cm. Trên cạnh AB, lấy điểm E sao cho AE = 10 cm. Trên cạnh AC, lấy điểm F sao cho AF = 8 cm (Hình 18a). Tính độ dài đoạn thẳng EF?
b) Trong Hình 18b, cho biết FD = FC, BC = 9 dm, DE = 12 dm, AC = 15 dm, MD = 20 dm. Chứng minh rằng ΔABCᔕΔMED?
Hướng dẫn giải chi tiết Bài 6
a) Xét tam giác AFE và ABC có:
- \(\frac{AF}{AB}=\frac{AE}{AC}=\frac{2}{3}\)
- \(\widehat{A}\) chung
Vậy \(\Delta AFEᔕ\Delta ABC\) (c.g.c)
Nên \(\frac{AF}{AB}=\frac{AE}{AC}=\frac{EF}{BC}=\frac{2}{3}\)
Suy ra \(EF = 12~cm\)
b) Xét tam giác ABC và MED ta có:
- \(\frac{BC}{ED}=\frac{AC}{MD}=\frac{3}{4}\)
- \(\widehat{C}=\widehat{D}\) (tam giác FDC cân)
Vậy \(\Delta ABCᔕ\Delta MED\) (c.g.c)
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài tập 4 trang 71 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 5 trang 71 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 7 trang 71 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 8 trang 72 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 9 trang 72 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 10 trang 72 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST





