Bài tập 4 trang 57 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST

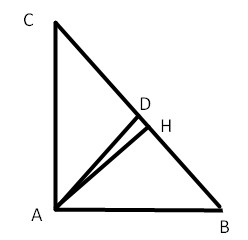
a) - Tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có:

\(BC^{2}=AC^{2}+AB^{2}\) suy ra \(BC = 5~cm\)

- AD là tia phân giác góc A nên \(\frac{DB}{DC}=\frac{AB}{AC}\)

\(\Rightarrow \frac{DB}{5-DB}=\frac{3}{4}\)

\(\Rightarrow 4DB=15-3DB\)

\(\Rightarrow DB=\frac{15}{7}\) (cm)

Do đó \(DC=BC-DB=5-\frac{15}{7}=\frac{20}{7}\) (cm)

b) - Ta có: \(S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}AH.BC\)

\(\Rightarrow AH=\frac{AB.AC}{BC}=\frac{3.4}{5}=\frac{12}{5}\) (cm)

- Tam giác ABH vuông tại H nên \(HB=\sqrt{AB^{2}-AH^{2}}=\sqrt{3^{2}-(\frac{12}{5})^{2}}=\frac{9}{5}\) (cm)

- Ta có: \(HD=DB-HB=\frac{15}{7}-\frac{9}{5}=\frac{12}{35}\) (cm)

- Tam giác ADH vuông tại H nên \(AD=\sqrt{HD^{2}+AH^{2}}=\sqrt{(\frac{12}{35})^{2}+(\frac{12}{5})^{2}}=\frac{12\sqrt{2}}{7}\) (cm)

-- Mod Toán 8 HỌC247