Bài tập 2 trang 57 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST

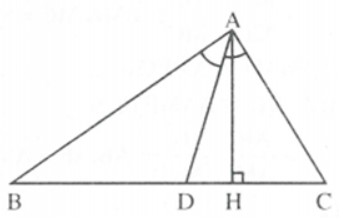
a) Tam giác ABC có AD là đường phân giác.

\(\Rightarrow \frac{DB}{AB}=\frac{DC}{AC}\)

\(\Rightarrow \frac{DB}{AB}=\frac{DC}{AC}=\frac{DB+DC}{AB+AC}=\frac{BC}{AB+AC}\)

\(\Rightarrow \frac{DB}{8}=\frac{DC}{6}=\frac{10}{8+6}\)

\(\Rightarrow DB=\frac{40}{7}~cm,BC=\frac{30}{7}~cm\)

b) Vẽ \(AH\perp BC\) tại H

\(\frac{S_{ABD}}{S_{ACD}}=\frac{\frac{1}{2}AH.DB}{\frac{1}{2}AH.DC}=\frac{DB}{DC}=\frac{\frac{40}{7}}{\frac{30}{7}}=\frac{4}{3}\)

-- Mod Toán 8 HỌC247