Giải bài 2.2 tr 159 sách BT Toán lớp 8 Tập 1
a. Dùng diện tích để chứng tỏ : \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\)
b. Dùng diện tích để chứng tỏ : \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\)với điều kiện b < a
Hướng dẫn giải chi tiết
Hướng dẫn giải
Dựng hình vuông rồi lấy các điểm và đặt độ dài sao cho phù hợp.
Sau đó áp dụng công thức tính diện tích hình chữ nhật : S=ab
Lời giải chi tiết
a. Dựng hình vuông ABCD có cạnh bằng (a + b )
Trên cạnh AB dựng điểm E sao cho AE = a, EB = b, trên cạnh BC dựng điểm H sao cho BH = b, HC = a, trên cạnh CD dựng điểm G sao cho CG = b, GD = a, trên cạnh DA dựng điểm K sao cho DK = a, KA = b, GE cắt KH tại F.
Ta có : diện tích hình vuông ABCD bằng \({\left( {a + b} \right)^2}\)
Diện tích hình vuông DKFG bằng \({a^2}\)
Diện tích hình chữ nhật AKFE bằng a.b
Diện tích hình vuông EBHF bằng \({b^2}\)
Diện tích hình chữ nhật HCGF bằng a.b
\({S_{ABCD}} = {S_{DKFG}} + {S_{AKFE}} + {S_{EBHF}} + {S_{HCGF}}\)
Vậy ta có : \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\)
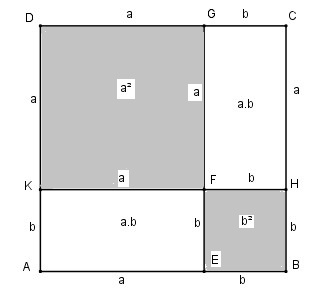
b. Dựng hình vuông ABCD có cạnh bằng a
Trên cạnh AB lấy điểm E sao cho BE = b
Từ E dựng đường thẳng song song BC cắt CD tại G
Ta có: CG = b, CE = ( a – b ), GD = ( a – b )
Trên cạnh AD lấy điểm K sao cho AK = b
Từ K kẻ đường thẳng song song với AB cắt BC tại H và cắt EG tại F
Ta có: KD = ( a – b ), BH = b
Hình vuông ABCD có diện tích bằng \({a^2}\)
Hình vuông DKFG có diện tích bằng \({\left( {a - b} \right)^2}\)
Hình chữ nhật AEFK có diện tích bằng ( a – b ) b
Hình vuông EBHF có diện tích bằng \({b^2}\)
Hình chữ nhật HCGF có diện tích bằng ( a – b ).b
\({S_{ABCD}} = {S_{DKFG}} + {S_{AEFK}} = {S_{EBHF}} + {S_{HCGF}}\)
nên \({\left( {a - b} \right)^2} + \left( {a - b} \right)b + \left( {a - b} \right)b + {b^2} = {a^2}\)
\(\Rightarrow {\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\)
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





