Bài 1 trang 103 SGK Toán 8 Tập 1 Cánh diều
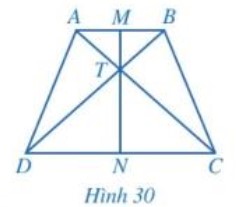
Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi M, N lần lượt là trung điểm của cạnh AB, CD và T là giao điểm của AC và BD (hình 30).
a) \(\widehat {TA{\rm{D}}} = \widehat {TBC},\widehat {T{\rm{D}}A} = \widehat {TCB}\).
b) \(TA = TB,T{\rm{D}} = TC\).
c) MN là đường trung trực của cả hai đoạn thẳng AB và CD.
Hướng dẫn giải chi tiết Bài 1
a) Xét \(\Delta ADC\) và \(\Delta BDC\) có:
DC là cạnh chung.
\(\widehat {ADC} = \widehat {BCD}\) (do ABCD là hình thang cân)
AD = BC
\( \Rightarrow \Delta ADC = \Delta BDC(c.g.c)\)
\( \Rightarrow \widehat {CAD} = \widehat {DBC}\) (2 góc tương ứng) hay
Do \(\Delta ADC = \Delta BDC\)
Xét \(\Delta BAD\) và \(\Delta ACB\) có:
AB chung
AD = BC
AC = BD
\( \Rightarrow \Delta BDA = \Delta ACB\) (c.c.c)
\( \Rightarrow \widehat {BDA} = \widehat {ACB}\) (2 góc tương ứng) hay \(\widehat {TDA} = \widehat {TCB}\)
b) Xét \(\Delta TAD\) và \(\Delta TBC\) có:
\(\widehat {TAD} = \widehat {TBC}\)(theo câu a)
AD = BC (ABCD là hình thang cân)
\(\widehat {TDA} = \widehat {TCB}\)(theo câu a)
\( \Rightarrow \Delta TAD = \Delta TBC \Rightarrow TA = TB,TC = TD\)
c) Vì TA = TB \( \Rightarrow \Delta ATB\) cân tại T suy ra TM là trung trực của AB.
TC = TD \( \Rightarrow \Delta DTC\) cân tại T suy ra TN là trung trực của CD
Mà: M, T, N thẳng hàng. Nên MN là đường trung trực của cả 2 đường thẳng AB và CD.
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





