Bài 2: Kiểm định giả thiết phương pháp khoảng tin cậy và trung bình của tổng thể

Giả sử ta cần kiểm định giả thiết: \({H_0}:\theta = {\theta _0};\,\,{H_1}:\theta \ne {\theta _0}\); trong đó \(\theta \) là tham số nào đó của một đại lượng ngẫu nhiên (kỳ vọng toán hoặc phương sai,....) ; \(\theta_0\) là một hằng số đã biết.

Theo phương pháp ước lượng khoảng, với độ tin cậy \(1-\alpha\) ta có thể tìm được khoảng \(\left( {\widehat {{\theta _1}};\widehat {{\theta _2}}} \right)\) sao cho:

\(P\left( {\widehat {{\theta _1}} < \theta < \widehat {{\theta _2}}} \right) = 1 - \alpha \)

Như vậy, với xác suất \(1-\alpha\), khoảng ngẫu nhiên \(\left( {\widehat {{\theta _1}};\widehat {{\theta _2}}} \right)\)chứa được \(\theta\). Vì \(1-\alpha\) lớn, nên theo nguyên lý xác suất lớn ta có thể coi biến cố \(\left( {\widehat {{\theta _1}} < \theta < \widehat {{\theta _2}}} \right)\) hầu như chắc chắn xảy ra trong một phép thử. Với một mẫu cụ thể (được coi là một phép thử) ta sẽ tính được một giá trị của \({\widehat {{\theta _1}}}\) (ký hiệu là \({\widehat {{\theta _1}}}^*\) ). Giá trị của \({\widehat {{\theta _2}}}\) cũng tính được và ký hiệu là \({\widehat {{\theta _2}}}^*\).

Nếu \(\theta \notin ({\widehat {{\theta _1}}^*};{\widehat {{\theta _2}}^*})\) thì ta bác bỏ H₀; Nếu \(\theta \in ({\widehat {{\theta _1}}^*};{\widehat {{\theta _2}}^*})\) thì ta chưa có cơ sở để bác bỏ H₀.

Thí dụ: Khảo sát hàm lượng Vitamin C của một loại trái cam (%) của một mẫu kích thước n = 100, người ta tính được:

\(\overline X = 9,45\% \) và s = 2,98496.

Gọi \(\mu\) là hàm lượng Vitamin C trung bình trong một trái của loại cam này. Hãy kiểm định giả thiết:

\({H_0}:\mu = 12\% ;{H_1}:\mu \ne 12\% \)

Với mức ý nghĩa 5%.

Giải: Với mức ý nghĩa \(\alpha = 5\%\) thì \(Z_{0 025} = 1,96\). Vậy khoảng tin cậy (với độ tin cậy 95%) của \(\mu\) là:

\(9,45 \pm 1,96\frac{{2,98946}}{{\sqrt {100} }}\) hay \((8,864 < \mu < 10,036)\)

Vì \(12 \notin (8,864;10,036)\) nên ta bác bỏ giả thiết H₀.

Tức hàm lượng Vitamin C trung bình trong một trái của loại cam này thấp hơn 12% (vì \(\overline X = 9,45 < 12\))

Giả sử trung bình của tổng thể (cũng chính là kỳ vọng toán của đại lượng ngẫu nhiên X) là \(\mu\) (\(\mu\) chưa biết), cần kiểm định giả thiết:

\(H_0:\mu=m_0\) với giả thiết đối \({H_1}:\mu \ne {m_0}\)

 (m₀ là một giá trị đã biết khi đặt giả thiết H₀).

Để kiểm định giả thiết trên ta tiến hành lấy mẫu với kích thức n và xét các trường hợp sau:

Trường hợp n \(\ge\) 30 (hoặc n <30 nhưng X có phân phối chuẩn) \({\sigma ^2}\) đã biết.

Trường hợp này ta chọn thống kê:  \(Z = \frac{{\overline X - {m_0}}}{{\sigma /\sqrt n }}\)  làm tiêu chuẩn kiểm định.

Nếu giả thiết H₀ đúng thì \(Z \sim N(0,1)\)

Với mức ý nghĩa \(\alpha\), chọn miền bác bỏ giả thiết H₀:

\({{\rm{W}}_\alpha } = \left\{ {z:\left| z \right| > {z_{\alpha /2}}} \right\}\)

Trong đó \({{z_{\alpha /2}}}\) là giá trị của Z ~ N(0, 1) thoả mãn:

\({z_{\alpha /2}} > 0\) và \(P\left( {\left| Z \right| > z{}_{\alpha /2}} \right) = \alpha \)

Trên đồ thị, miền bác bỏ \(W_{\alpha}\) được minh họa như sau:

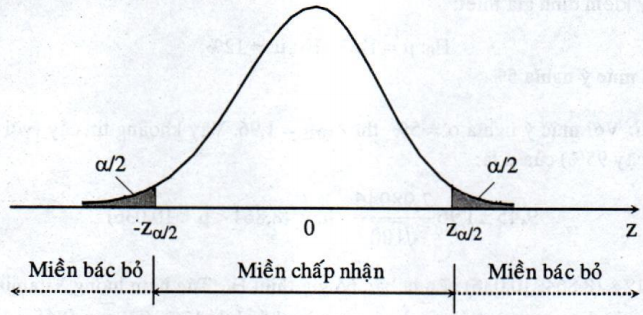
để xác định \({z{}_{\alpha /2}}\) ta tra bảng ở phần phụ lục hoặc dùng hàm NORMSINV trong Excel (xem phụ lục 1)

Ta có:

\(P\left( {Z \in {{\rm{W}}_\alpha }} \right) = P\left( {\left| Z \right| > {z_{\alpha /2}}} \right) = P\left( {Z < - {z_{\alpha /2}}} \right) + P\left( {Z > {z_{\alpha /2}}} \right) = \alpha /2 + \alpha /2 = \alpha \)

Như vậy xác suất để giá trị của Z rơi vào miền bác bỏ là \(\alpha\), tức xác suất để Z rơi vào miền chấp nhận sẽ là \(1-\alpha\). Vì \(\alpha\) nhỏ, nên xác suất để Z rơi vào miền chấp nhận sẽ lớn. Nghĩa là: nếu giả thiết H₀ đúng thì có thể coi rằng hầu hết các giá trị của Z sẽ rơi vào miền chấp nhận. Còn nếu giá trị của Z rơi vào miền bác bỏ có nghĩa là ta đã tìm được “bằng chứng” để chứng tỏ giả thiết H₀ là không đúng và vì thế ta bác bỏ giả thiết đó.

Từ đó ta có qui tắc quyết định khi tiến hành kiểm định giả thiết H₀ trong trường hợp này như sau: 

Lấy mẫu có kích thước n, từ mẫu cụ thể này tính \(z = \frac{{\left( {\overline X - {m_0}} \right)}}{\sigma }\sqrt n \)

(Trong đó \({\overline X }\) là trung bình mẫu).

Với mức ý nghĩa \(\alpha\) cho trước, xác định \(Z_{\alpha/2}\)

(bằng cách tra bảng ở phần phụ lục hoặc dùng hàm NORMSINV trong Excel)

• Nếu \(\left| z \right| > {z_{\alpha /2}}\). Tức \(z \in {{\rm{W}}_\alpha }\) thì ta bác bỏ giả thiết H₀, chấp nhận H₁.
• Nếu \(\left| z \right| \le {z_{\alpha /2}}\). Tức \(z \notin {{\rm{W}}_\alpha }\) thì có thể chấp nhận giả thiết H₀

Từ việc chấp nhận (hay bác bỏ) H₀ ta suy ra kết luận cuối cùng theo yêu cầu của bài toán thực tế.

Thí dụ 1: Nếu máy móc làm việc bình thường thì trọng lượng của một loại sản phẩm là đại lượng ngẫu nhiên có kỳ vọng toán là 100 gr. Qua một thời gian sản xuất, người ta nghi ngờ trọng lượng trung bình của loại sản phẩm này đã thay đổi. Cân thử 100 sản phẩm và tính được \(\overline X = 100,3\) gr và s = 1.

Với mức ý nghĩa \(\alpha = 0,05\)  hãy kết luận điều nghi ngờ trên có đúng hay không?

Giải: Gọi trọng lượng trung bình thực tế của loại sản phẩm đó sau một thời gian sản xuất là \(\mu\) (\(\mu\) chưa biết). Đặt giả thiết:

\({H_0}:\mu = 100;{H_1}:\mu \ne 100\)

Để kiểm định giả thiết này ta áp dụng qui tắc kiểm định nêu trên (vì kích thước mẫu n = 100 > 30; \(\sigma \) chưa biết)

\(Z = \frac{{(100,3 - 100)}}{1}\sqrt {100} = 3\)

Với mức ý nghĩa \(\alpha=0,05\) tra bảng ta được \(z_{0,025}=1,96\)

Vì \(\left| z \right| = 3 > {z_{0,025}} = 1,96\) nên ta bác bỏ giả thiết H₀. Tức điều nghi ngờ trên là đúng, trọng lượng trung bình của loại sản phẩm này đã khác 100 gr thực sự.

Chú ý:

Nếu kiểm định giả thiết \({H_0}:\mu = {m_0}\); và giả thiết đối \({H_0}:\mu > {m_0}\) với mức ý nghĩa \(\alpha\) thì chọn miền bác bỏ giả thiết H₀ là:

\({{\rm{W}}_\alpha } = \left\{ {z = \frac{{\overline x - {m_0}}}{{\sigma /\sqrt n }}:z > {z_\alpha }} \right\}\)

trong đó \(z_{\alpha}\) là giá trị của ĐLNN Z ~ N(0; 1) thỏa mãn:

\({z_\alpha } > 0\) và \(P\left( {\left| Z \right| > {z_\alpha }} \right) = \alpha \)

Trên đồ thị, miền bác bỏ \(W_{\alpha}\) trong trường hợp này được minh họa như sau:

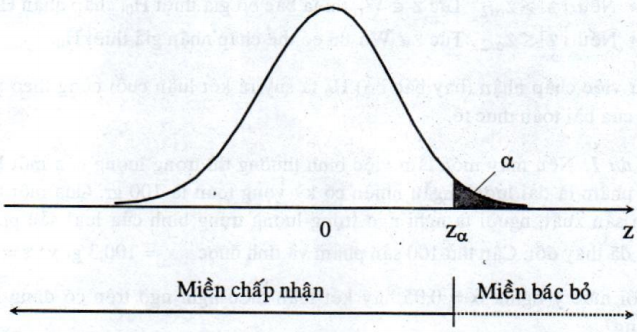
Nếu kiểm định giả thiết \({H_0}:\mu = {m_0}\); và giả thiết đối \({H_1}:\mu < {m_0}\) với mức ý nghĩa a thì chọn miền bác bỏ giả thiết H₀ là:

\({{\rm{W}}_\alpha } = \left\{ {z = \frac{{\overline x - {m_0}}}{{\sigma /\sqrt n }}:z < - {z_\alpha }} \right\}\)

Trên đồ thị, miền bác bỏ \(W_{\alpha}\) trong trường hợp này được minh họa như sau:

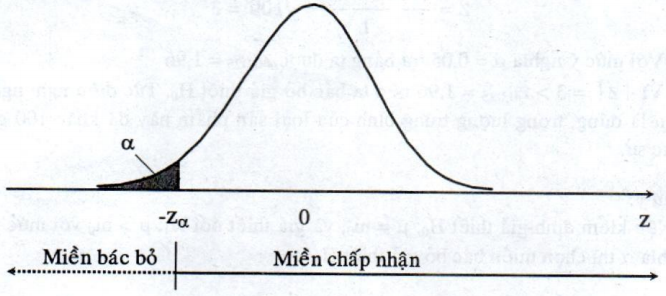
Trường hợp n \(\ge\) 30; \({\sigma ^2}\) chưa biết

Trường hợp này chọn: \(Z = \frac{{(\overline X - {m_0})}}{S}\sqrt n \) làm tiêu chuẩn kiểm định.

Nếu H₀ đúng thì Z ~ N(0, 1), do đó miền bác bỏ giả thiết H₀ và qui tắc quyết định trong trường hợp này tương tự như trường hợp trên. Chỉ khác là giá trị z được tính theo công thức:

\(z = \frac{{(\overline x - {m_0})}}{{s/\sqrt n }}\)

Chú ý:

Nếu kiểm định giả thiết: \({H_0}:\mu = {m_0};{H_1}:\mu \ne {m_0}\) Trường hợp bác bỏ giả thiết H₀

• Nếu \(\overline x < {m_0}\) thì có thể kết luận \(\mu < {m_0}\)
• Nếu \(\overline x > {m_0}\) thì có thể kết luận \(\mu > {m_0}\)

Trường hợp n < 30, \({\sigma ^2}\) chưa biết, X có phân phối chuẩn

Trường hợp này chọn: \(T = \frac{{(\overline X - {m_0})}}{S}\sqrt n \) làm tiêu chuẩn kiểm định. Nếu H₀ đúng thì T phân phối theo qui luật Student với n-1 bậc tự do.

Ta có thể minh họa miền bác bỏ với các dạng giả thiết đối khác nhau trên đồ thị như sau:

Nếu kiểm định giả thiết hai phía, tức giả thiết đối có dạng: \({H_1}:\mu \ne {m_0}\) thì miền bác bỏ \(W_{\alpha}\) được minh họa trên đồ thị như sau:

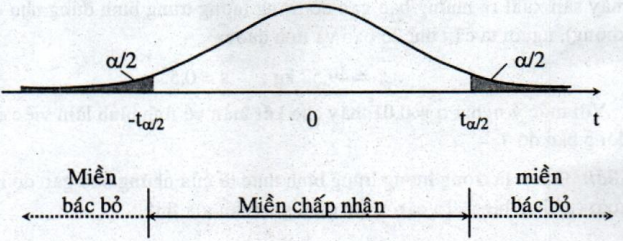
Nếu kiểm định giả thiết một phía với giả thiết đối có dạng: \({H_1}:\mu > {m_0}\) thì miền bác bỏ  được minh họa trên đồ thị như sau:

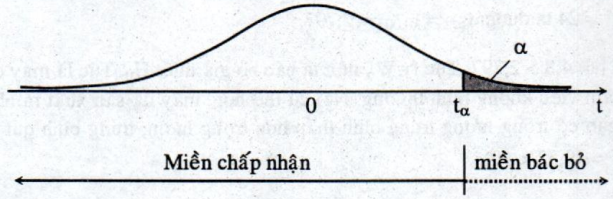
Nếu kiểm định giả thiết một phía với giả thiết đối có dạng: \({H_1}:\mu < {m_0}\) thì miền bác bỏ \(W_{\alpha}\) được minh họa trên đồ thị như sau:

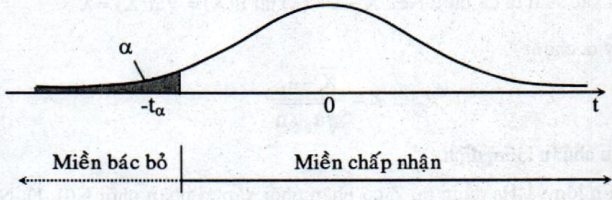
Thí dụ 2: Trọng lượng của các bao gạo do một máy đóng bao sản xuất là đại lượng ngẫu nhiên có phân phối chuẩn với trọng lượng trung bình qui định là 50 kg. Để xem máy đóng bao làm việc có bình thường không (theo nghĩa máy sản xuất ra những bao gạo có trọng lượng trung bình đúng như qui định không), người ta cân thử 25 bao và tính được:

\(\overline x = 49,52kg;s = 0,5\)

Với mức ý nghĩa \(\alpha\) = 0,01, hãy cho kết luận về tình hình làm việc của máy đóng bao đó?

Giải: Gọi \(\mu\) là trọng lượng trung bình thực tế của những bao gạo do máy sản xuất (\(\mu\) chưa biết). Ta cần kiểm định giả thiết giả thiết:

\({H_0}:\mu = 50;{H_1}:\mu \ne 50\)

Trường hợp này kích thước mẫu \(n = 25 < 30;{\sigma ^2}\) chưa biết.

\(t = \frac{{(49,52 - 50)}}{{0,5}}\sqrt {25} = - 4,8\)

Với mức ý nghĩa \(\alpha = 0,01\), tra bảng phân phối Student với bậc tự do là 25 - 1 = 24 ta được: \(t_{\alpha/2} = t_{0,005} = 2,797\).

Vì \(|t| = 4,8 > 2,797\). Tức \(t \in {{\rm{W}}_\alpha }\) nên ta bác bỏ giả thiết H₀. Tức là máy đóng bao làm việc không bình thường. Nói cụ thể hơn, máy đã sản xuất ra những bao gạo có trọng lượng trung bình thấp hơn ưọng lượng trung bình qui định (vì \(\overline x = 49,52 < 50\)).

Trường hợp n\(\ge\)30; X có phân phôi Poisson

Giả sử đại lượng ngẫu nhiên X có phân phối Poisson với E(X) = \(\lambda \) chưa biết. Cần kiểm định giả thiết:

\({H_0}:\lambda = {a_0};{H_1}:\lambda \ne {a_0}\)

Do vậy ta chọn: 

\(Z = \frac{{\overline X - {a_0}}}{{\sqrt {{a_0}/n} }}\)

làm tiêu chuẩn kiểm định.

Nếu n lớn và H₀ đúng thì Z có phân phối xấp xỉ phân phối N(0, 1). Nên miền bác bỏ và qui tắc kiểm định giống trường hợp 2.1. Chỉ khác là trong qui tắc kiểm định ta tính z theo công thức sau:

\(z = \frac{{(\overline x - {a_0})\sqrt n }}{{\sqrt {{a_0}} }}\)

Thí dụ 3: số người đến một trung tâm thương mại trong những khoảng thời gian 5 phút là đại lượng ngẫu nhiên X có phân phối Poisson. Trong mùa mưa, người ta xác định được E(X) = 4. Sang mùa khô, theo dõi 36 khoảng thời gian, (mỗi khoảng 5 phút) người ta thấy có 174 người đến trung tâm này.

Yới mức ý nghĩa \(\alpha = 0,05\), hãy xét xem khí hậu có ảnh hưởng đến số người tới trung tâm thương mại đó hay không?

Giải: Gọi số người tới trung tâm thương mại trung bình trong khoảng thời gian 5 phút là X, (X, chưa biết). Đặt giả thiết:

\({H_0}:\lambda = 4;{H_1}:\lambda \ne 4\)

Với mức ý nghĩa \(\alpha = 0,05\) thì \(Z_{0,025} = 1,96\).

Theo giả thiết bài toán ta tính được số người đến trung tâm trung bình trong khoảng thời gian 5 phút của mẫu là:

\(\overline x = \frac{{174}}{{36}} = 4,833\)

Vậy: 

\(z = \frac{{\left( {4,833 - 4} \right)\sqrt {36} }}{{\sqrt 4 }} = 2,499\)

Ta thấy |z| > 1,96 nên ta bác bỏ giả thiết H₀. Nghĩa là khí hậu có ảnh hưởng tới dòng người đến trung tâm thương mại đó.