Mời các bạn cùng tham khảo nội dung bài giảng Bài 2: Các tham số đặc trưng của đại lượng ngẫu nhiên (phần 3) sau đây để tìm hiểu về giá trị tin chắc nhất, một số tham số đặc trưng khác.
Tóm tắt lý thuyết
3. Độ lệch chuẩn
Ngoài phương sai ra, người ta còn sử dụng một tham số khác để đặc trưng cho mức độ phân tán của đại lượng ngẫu nhiên, đó là độ lệch chuẩn.
Độ lệch chuẩn của đại lượng ngẫu nhiên X [ký hiệu là \(\sigma \) (X)] là căn bậc 2 của phương sai:
\(\sigma (X) = \sqrt {V{\rm{ar}}(X)} \)
Ta thấy rằng đơn vị đo của phương sai bằng bình phương đơn vị đo của đại lượng ngẫu nhiên. Vì vậy khi cần phải đánh giá mức độ phân tán các giá trị của đại lượng ngẫu nhiên theo đơn vị đo của nó, người ta thường dùng độ lệch tiêu chuẩn, vì độ lệch tiêu chuẵn có cùng đơn vị đo với đại lượng ngẫu nhiên đang nghiên cứu.
4. Giá trị tin chắc nhất
Định nghĩa: Giá trị tin chắc nhất của đại lượng ngẫu nhiên rời rạc X [ký hiệu là Mod(X)] là giá trị của X ứng với xác suất lớn nhất ưong bảng phân phối xác suất.
Nếu X là đại lượng ngẫu nhiên liên tục có hàm mật độ xác suất f(x) thì Mod(X) là giá trị của X mà tại đó hàm mật độ đạt giá trị cực đại.
Thí dụ: Đại lượng ngẫu nhiên X có qui luật phân phối xác suất như sau:
| X | 7 | 8 | 9 | 10 | 11 | 12 | 14 |
| P | 0,1 | 0,14 | 0,3 | 0,24 | 0,11 | 0,06 | 0,05 |
Ta thấy P(X = 9) = 0,3 lớn nhất. Vì vậy Mod(X) = 9
Từ định nghĩa của Mod(X) ta thấy Mod(X) chính là giá trị có khả năng xảy ra nhiều nhất trong các giá trị mà đại lượng ngẫu nhiên X có thể nhận. Chẳng hạn, X là chiều cao của sinh viên trong một trường, thì Mod(X) là chiều cao mà nhiều sinh viên đạt được nhất; Nếu Y là năng suất của những công nhân trong một nhà máy thì Mod(Y) là năng suất mà số công nhân đạt được mức năng suất này ở nhà máy là nhiều nhất...
Chú ý: Mod(X) có thể nhận nhiều giá trị khác nhau.
Thí dụ: Đại lượng ngẫu nhiên Y có phân phối xác suất như sau:
| Y | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P | 0,1 | 0,15 | 0,3 | 0,3 | 0,08 | 0,05 | 0,02 |
Ta thấy xác suất lớn nhất trong bảng trên là 0,3 ứng với hai giá trị Y = 3 và Y = 4. Vậy Mod(Y) = 3 hoặc Mod(Y) = 4.
5. Một số tham số đặc trưng khác
5.1 Mô men
Định nghĩa 1: Mô men gốc cấp k (ký hiệu là \({\alpha _k}\)) được định nghĩa như sau:
\({\alpha _k} = E\left| {{{(X)}^k}} \right|\)
Định nghĩa 2: Mô men trung tâm cấp k (ký hiệu là \({\mu _k}\)) được định nghĩa như sau:
\({\mu _k} = E\left\{ {{{\left[ {X - E(X)} \right]}^k}} \right\}\)
Như vậy, kỳ vọng toán chính là mô men gốc cấp 1: \(E(X) = {\alpha _1}\) ; Phương sai chính là mô men trung tâm cấp 2: \(v{\rm{ar(X) = }}{\mu _2}\)
Giữa mô men gốc và mô men trung tâm có mối liên hệ như sau:
- \({\mu _2} = v{\rm{ar}}(X) = E({X^2}) - {\left[ {E(X)} \right]^2} = {\alpha _2} - {({\alpha _1})^2}\)
- \({\mu _3} = {\alpha _3} - 3{\alpha _1}{\alpha _2} + 2{({\alpha _1})^3}\)
- \({\mu _4} = {\alpha _4} - 4{\alpha _1}{\alpha _3} + 6{({\alpha _1})^2}{\alpha _2} - 3{({\alpha _1})^4}\)
5.2 Hệ số bất đối xứng
Ta định nghĩa: \(S = \frac{{{\mu _3}}}{{{\sigma ^3}}}\)
Là hệ số bất đối xứng của đại lượng ngẫu nhiên X (trong đó \(\sigma \) là độ lệch chuẩn.
Xét biểu thức của \({{\mu _3}}\) ta có: \({\mu _3} = E\left\{ {{{\left[ {X - E(X)} \right]}^3}} \right\} = {\int\limits_{ - \infty }^{ + \infty } {\left[ {x - E(X)} \right]} ^3}f(x)dx\)
Bằng phép tịnh tiến trục Oy đến đường thẳng X = E(X) ta thấy:
Nếu đồ thị của hàm mật độ f(x) đối xứng qua đường thẳng X = E(X) thì \({\mu _3}=0\) (hình 2.6)

hình 2.6
Nếu \({\mu _3}>0\) thì đồ thị của hàm mật độ f(x) không đối xứng qua đường thẳng X = E(X), phân phối của X lệch về phía bên phải, (hình 2.7)
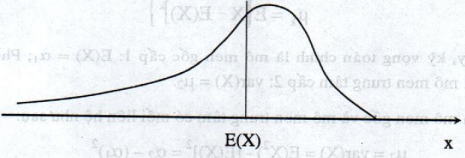
Hình 2.7
Nếu \({\mu _3}<0\) thì đồ thị của hàm mật độ f(x) không đối xứng qua đường thẳng X = E(X), phân phối của X lệch về phía bên trái, (hình 2.8)
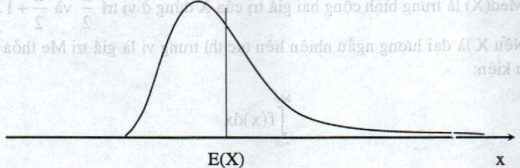
Hình 2.8
5.3 Hệ số nhọn
Ta định nghĩa: \(K = \frac{{{\mu _4}}}{{{\sigma _4}}}\)
Là hệ số nhọn của đại lượng ngẫu nhiên X. Nếu K càng lớn thì đồ thị hàm mật độ của đại lượng ngẫu nhiên đó càng nhọn, (hình 2.9)

Hình 2.9
5.4 Trung vị
Trung vị của đại lượng ngẫu nhiên X [Ký hiệu là Med(X)] là giá trị chia phân phối của đại lượng ngẫu nhiên thành hai phần bằng nhau.
Nếu X là đại lượng ngẫu nhiên rời rạc, ta có thể sắp xếp các giá trị của X (và quan tâm đến số lần lặp lại của X) thành một dãy số theo thứ tự từ 1 đến n. Nếu n lẻ thì Med(X) là giá trị của X đứng ở vị trí thứ \(\frac{{n + 1}}{2}\); Nếu n chẵn thì Med(X) là trung bình cộng hai giá trị của X đứng ở vị trí\(\frac{{n }}{2}\) và
Nếu X là đại lượng ngẫu nhiên liên tục thì trung vị là giá trị Me thỏa mãn điều kiện:
\(\int\limits_{ - \infty }^{Me} {f(x)dx} \)
Thí dụ 1: Cho đại lượng ngẫu nhiên X có bảng phân phối xác suất như sau:
| X | 0 | 1 | 2 |
| P | 2/15 | 8/15 | 5/15 |
Tìm Med(X)
Giải: Sắp xếp các giá trị của X theo thứ tự tăng dần và có chú ý đến số lần lặp lại của X ta được:
| Số TT | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| X | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 |
Theo bảng trên, n = 15;
X nhận giá trị 0 được lặp lại 2 lần; [vì P(X = 0) = 2/15];
X nhận giá trị 1 được lặp lại 8 lần; [vì P(X = 1) = 8/15];
X nhận giá trị 2 được lặp lại 5 lần; [vì P(X = 2) = 5/15];
Vì n lẻ (n =15) nên Med(X) = 1 (1 là giá trị của X đứng ở vị trí thứ 8)
Thí dụ 2: Cho đại lượng ngẫu nhiên Y có quy luật phân phối xác suất như sau:
| Y | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| P | 0,06 | 0,14 | 0,3 | 0,2 | 0,1 | 0,12 | 0,08 |
Tìm Med(Y).
Giải: Sắp xếp các giá trị của Y theo thứ tự tăng dần và có chú ý đến số lần lặp lại của Y ta được:
| Số TT | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Y | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 |
| Số TT | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| Y | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 6 |
| STT | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| Y | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 7 | 7 | 7 |
| STT | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| Y | 7 | 8 | 8 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 |
Trong bảng trên giá trị Y=3 được lặp lại 3 lần vì P(Y=3) = 0,06 =3/50 giá trị Y = 4 được lặp lăi 7 lần vì P(Y = 4) = 0,14 = 7/50;....
Vì n chẵn (n = 50) nên Med(Y) là trung bình cộng của 5 và 6 (là hai giá trị của Y nằm ở vị trí 25 và 26).
Vậy: Međ(Y) = 5,5
Chú ý: Để tính Med(X) ta có thể dùng hàm MEDIAN trong Excel









