Mß╗Øi c├Īc bß║Īn c├╣ng tham khß║Żo nß╗Öi dung b├Āi giß║Żng B├Āi 2: Suy luß║Łn diß╗ģn dß╗ŗch phß║¦n tiß║┐p theo sau ─æ├óy ─æß╗ā t├¼m hiß╗āu vß╗ü uy diß╗ģn gi├Īn tiß║┐p vß╗øi tiß╗ün ─æß╗ü phß╗®c hß╗Żp, quy tß║»c suy diß╗ģn.
T├│m tß║»t l├Į thuyß║┐t
4. Suy diß╗ģn gi├Īn tiß║┐p vß╗øi tiß╗ün ─æß╗ü phß╗®c hß╗Żp
TrŲ░ß╗Øng hß╗Żp tiß╗ün ─æß╗ü l├Ā ph├Īn ─æo├Īn c├│ ─æiß╗üu kiß╗ćn
Nß║┐u cß║Ż hai tiß╗ün ─æß╗ü ─æß╗üu l├Ā ph├Īn ─æo├Īn c├│ ─æiß╗üu kiß╗ćn th├¼ ngŲ░ß╗Øi ta gß╗Źi l├Ā suy diß╗ģn c├│ ─æiß╗üu kiß╗ćn thuß║¦n t├║y.
Th├Ł dß╗ź:
- Nß║┐u trß╗Øi (S1) mŲ░a (P1) th├¼ ─æŲ░ß╗Øng (S2) Ų░ß╗øt. (P2)
- Nß║┐u ─æŲ░├▓ng (S2) Ų░ß╗øt (P2) th├¼ bß║®n. (P2)
ŌćÆ Vß║Ły, nß║┐u trß╗Øi (S1) mŲ░a (P1) th├¼ bß║®n. (P3)
H├¼nh thß╗®c l├┤gic c├│ dß║Īng nhŲ░ sau:
- (S1 ŌĆō P1) ŌåÆ (S2 - P2)
- (S2 - P2)ŌåÆ (S1 - P3)
ŌćÆ Vß║Ły, (S1 ŌĆō P1)ŌåÆ(S1 ŌĆō P3).
Suy diß╗ģn kiß╗āu nhŲ░ tr├¬n thß╗▒c chß║źt dß╗▒a tr├¬n t├Łnh bß║»c cß║¦u cß╗¦a ph├®p k├®o theo. Nß║┐u biß╗āu diß╗ģn mß╗Śi ph├Īn ─æo├Īn ─æŲĪn bß║▒ng c├Īc chß╗» p, q, r..., th├¼ suy diß╗ģn c├│ ─æiß╗üu kiß╗ćn thuß║¦n t├║y sß║Į c├│ h├¼nh thß╗®c l├┤gic nhŲ░ sau:
\(\frac{\begin{array}{l} p \to q\\ q \to r \end{array}}{{p \to r}}\)
Suy diß╗ģn nhß║źt quyß║┐t c├│ ─æiß╗üu kiß╗ćn l├Ā suy diß╗ģn c├│ ─æiß╗üu kiß╗ćn trong ─æ├│ mß╗Öt tiß╗ün ─æß╗ü l├Ā ph├Īn ─æo├Īn c├│ ─æiß╗üu kiß╗ćn, tiß╗ün ─æß╗ü kia l├Ā ph├Īn ─æo├Īn nhß║źt quyß║┐t ─æŲĪn kiß╗āu A, E, O, I. Loß║Īi suy diß╗ģn n├Āy c├│ hai phŲ░ŲĪng thß╗®c: khß║│ng ─æß╗ŗnh hoß║Ęc l├Ā phß╗¦ ─æß╗ŗnh.
PhŲ░ŲĪng thß╗®c khß║│ng ─æß╗ŗnh c├│ hai dß║Īng
- Khß║»ng ─æß╗ŗnh tuyß╗ćt ─æß╗æi phi tinh th├Īi
Th├Ł dß╗ź:
Nß║┐u trß╗Øi mŲ░a (p) th├¼ ─æŲ░ß╗Øng Ų░ß╗øt. (q)
Trß╗Øi mŲ░a. (p)
ŌćÆ Vß║Ły, ─æŲ░ß╗Øng Ų░ß╗øt. (q)
- Khß║│ng ─æß╗ŗnh tŲ░ŲĪng ─æß╗æi t├¼nh th├Īi
Th├Ł dß╗ź:
Nß║┐u trß╗Øi mŲ░a (p) th├¼ ─æŲ░ß╗Øng Ų░ß╗øt. (q)
─ÉŲ░ß╗Øng Ų░ß╗øt (q)
ŌćÆ Vß║Ły, c├│ thß╗ā l├Ā do trß╗Øi mŲ░a (p)
Nß║┐u ta k├Į hiß╗ću t├¼nh th├Īi khß║Ż n─āng "c├│ thß╗ā" dŲ░ß╗øi dß║Īng bß║▒ng k├Į hiß╗ću th├¼ h├¼nh thß╗®c l├┤gic cß╗¦a t├Łnh tŲ░ŲĪng ─æß╗æi t├¼nh th├Īi c├│ dß║Īng nhŲ░ sau:
PhŲ░ŲĪng thß╗®c phß╗¦ ─æß╗ŗnh c┼®ng c├│ hai dß║Īng
- Phß╗¦ ─æß╗ŗnh tuyß╗ćt ─æß╗æi phi tinh th├Īi
Th├Ł dß╗ź:
Nß║┐u trß╗Øi mŲ░a (p) th├¼ ─æŲ░ß╗Øng Ų░ß╗øt.(q)
─ÉŲ░ß╗Øng kh├┤ng Ų░ß╗øt (q)
ŌćÆ Vß║Ły, trß╗Øi kh├┤ng mŲ░a (p)
- Phß╗¦ ─æß╗ŗnh tŲ░ŲĪng ─æß╗æi t├¼nh th├Īi
Th├Ł dß╗ź:
Nß║┐u trß╗Øi mŲ░a (p) th├¼ ─æŲ░ß╗Øng Ų░ß╗øt. (q)
Trß╗Øi kh├┤ng mŲ░a. (p)
ŌćÆ Vß║Ły, c├│ thß╗ā ─æŲ░ß╗Øng kh├┤ng Ų░ß╗øt (q)
Ta c├│ thß╗ā kiß╗ām tra gi├Ī trß╗ŗ ch├ón l├Į cß╗¦a c├Īc c├┤ng thß╗®c:
(1) \((p \to q) \wedge p \to q \)
(2) \((p \to q) \wedge \overline q \to \overline p \)
Bß║Żng gi├Ī trß╗ŗ ch├ón l├Į:
| p | q | \(\overline p \) | \(\overline q\) | pŌåÆq | \((p \to q) \wedge p\) | \((p \to q) \wedge p \to q\) | \((p \to q) \wedge \overline q \) | \((p \to q) \wedge \overline q \to \overline p \) |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
Ta thß║źy 2 c├┤ng thß╗®c n├¬u tr├¬n ─æß╗üu l├Ā hß║▒ng ch├ón, ngh─®a l├Ā biß╗āu thß╗ŗ quy luß║Łt l├┤g├Łc lŲ░ß╗Īng trß╗ŗ. Do ─æ├│, c├│ thß╗ā sß╗Ł dß╗źng l├Ām quy tß║»c suy diß╗ģn hay c├▓n gß╗Źi l├Ā: quy tß║»c kß║┐t luß║Łn.
Quy tß║»c khß║│ng ─æß╗ŗnh (gß╗Źi l├Ā modus ponens), thß╗▒c hiß╗ćn theo lŲ░ß╗Żc ─æß╗ō l├┤gic sau ─æ├óy:
pŌåÆq, p .png) q
q
pŌåÆq, q 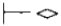 p
p
Quy t├Īc phß╗¦ ─æß╗ŗnh (gß╗Źi l├Ā modus tollens) thß╗▒c hiß╗ćn theo lŲ░ß╗Żc ─æß╗ō l├┤gic sau ─æ├óy:
pŌåÆq, \(\overline q \) .png) \(\overline p\)
\(\overline p\)
pŌåÆq, \(\overline p\) 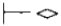 \(\overline q\)
\(\overline q\)
TrŲ░ß╗Øng hß╗Żp tiß╗ün ─æß╗ü l├Ā ph├Īn ─æo├Īn lß╗▒a chß╗Źn (ph├ón liß╗ćt)
Trong mß╗Öt suy luß║Łn, nß║┐u cß║Ż hai tiß╗ün ─æß╗ü ─æß╗üu l├Ā ph├Īn ─æo├Īn lß╗▒a chß╗Źn ngŲ░ß╗Øi ta gß╗Źi l├Ā suy diß╗ģn ph├ón liß╗ćt thuß║¦n t├║y.
Th├Ł dß╗ź:
- H├┤m nay B├¼nh (s) phß║Żi hß╗Źc to├Īn (p) hoß║Ęc hß╗Źc sß╗Ł (r) hoß║Ęc hß╗Źc v─ān. (q)
- Nß║┐u hß╗Źc to├Īn (p) th├¼ phß║Żi hß╗Źc ─æß║Īi sß╗æ (p1) hoß║Ęc hß╗Źc h├¼nh hß╗Źc. (p2)
ŌćÆ Vß║Ły h├┤m nay B├¼nh (s) phß║Żi hß╗Źc ─æß║Īi sß╗æ (p1) hoß║Ęc h├¼nh hß╗Źc (p2) hoß║Ęc hß╗Źc v─ān (q) hoß║Ęc hß╗Źc sß╗Ł (r)
H├¼nh thß╗®c l├┤gic c├│ dß║Īng sau:
- s l├Ā p hoß║Ęc q hoß║Ęc r.
- p l├Ā p1 hoß║Ęc p2,
ŌćÆ Vß║Ły s l├Ā p1 hoß║Ęc p2 hoß║Ęc q hoß║Ęc r.
Nß║┐u k├Į hiß╗ću ph├Īn ─æo├Īn ─æŲĪn dŲ░ß╗øi dß║Īng p, q. r,... th├¼ sß║Į c├│ dß║Īng:
\(\frac{\begin{array}{l} p \vee q \vee r\\ {p_1} \vee {p_2} \end{array}}{{{p_1} \vee {p_2} \vee q \vee r}}\)
Suy diß╗ģn nhß║źt quyß║┐t ph├ón liß╗ćt l├Ā suy diß╗ģn ph├ón liß╗ćt, trong ─æ├│ mß╗Öt tiß╗ün ─æß╗ü l├Ā ph├Īn ─æo├Īn ph├ón liß╗ćt, c├▓n tiß╗ün ─æß╗ü kia l├Ā ph├Īn ─æo├Īn nhß║źt quyß║┐t.
C├│ hai phŲ░ŲĪng thß╗®c khß║│ng ─æß╗ŗnh ─æß╗ā phß╗¦ ─æß╗ŗnh v├Ā phß╗¦ ─æß╗ŗnh ─æß╗ā khß║│ng dinh
PhŲ░ŲĪng thß╗®c khß║│ng ─æß╗ŗnh - phß╗¦ ─æß╗ŗnh
Th├Ł dß╗ź:
- C├Īc g├│c trong cß╗¦a tam gi├Īc c├│ thß╗ā nhß╗Źn hoß║Ęc t├╣ hoß║Ęc vu├┤ng.
- G├│c n├Āy cß╗¦a tam gi├Īc ─æ├Ż cho l├Ā g├│c nhß╗Źn.
ŌćÆ Vß║Ły n├│ kh├┤ng phß║Żi l├Ā g├│c t├╣ c├╣ng kh├┤ng phß║Żi l├Ā g├│c vu├┤ng.
PhŲ░ŲĪng thß╗®c phß╗¦ ─æß╗ŗnh - khß║│ng ─æß╗ŗnh
Th├Ł dß╗ź:
- Ph├ón b├│n v├┤ cŲĪ c├│ thß╗ā l├Ā ph├ón Kali hoß║Ęc NitŲĪ hoß║Ęc Phß╗æt pho.
- Bao ph├ón b├│n v├┤ cŲĪ n├Āy kh├┤ng phß║Żi l├Ā ph├ón NitŲĪ, m├Ā c┼®ng kh├┤ng phß║Żi l├Ā ph├ón Phß╗æt pho.
ŌćÆ Vß║Ły, n├│ l├Ā ph├ón Kali.
Suy diß╗ģn phß║½n liß╗ćt c├│ ─æiß╗üu kiß╗ćn hay giß║Ż ─æß╗ŗnh lß╗▒a chß╗Źn
─É├óy l├Ā loß║Īi suy diß╗ģn, trong ─æ├│ mß╗Öt tiß╗ün ─æß╗ü l├Ā ph├Īn ─æo├Īn c├│ ─æiß╗üu kiß╗ćn, tiß╗ün ─æß╗ü kia l├Ā ph├Īn ─æo├Īn ph├ón liß╗ćt. Dß║Īng ─æŲĪn giß║Żn l├Ā hai th├Ānh phß║¦n, phß╗®c tß║Īp hŲĪn l├Ā 3, hoß║Ęc nhiß╗üu th├Ānh phß║¦n hŲĪn.
X├®t trŲ░ß╗Øng hß╗Żp hai th├Ānh phß║¦n
C├│ hai phŲ░ŲĪng thß╗®c phß╗¦ ─æß╗ŗnh v├Ā khß║│ng ─æß╗ŗnh.
PhŲ░ŲĪng thß╗®c khß║│ng ─æß╗ŗnh (kiß║┐n thiß║┐t)
Th├Ł dß╗ź:
- Nß║┐u bß╗ŗ ─æau r─āng th├¼ n├¬n uß╗Ģng thuß╗æc giß║Żm ─æau Analgesic.
- Nß║┐u ─æau ─æß║¦u th├¼ n├¬n uß╗æng thuß╗æc giß║Żm ─æau Analgesic.
- NgŲ░ß╗Øi n├Āy ─æau r─āng hoß║Ęc ─æau ─æß║¦u.
ŌćÆ Vß║Ły, ngŲ░ß╗Øi n├Āy n├¬n d├╣ng thuß╗æc giß║Żm ─æau Analgesic.
─É├óy l├Ā c├┤ng thß╗®c hß║▒ng ch├ón (luß║Łt l├┤gic), cho n├¬n c├│ thß╗ā d├╣ng l├Ām quy tß║»c suy diß╗ģn.
\((p \to q) \wedge (r \to q) \wedge (p \vee r)\) .png) q
q
TrŲ░ß╗Øng hß╗Żp tiß╗ün ─æß╗ā l├Ā ph├Īn ─æo├Īn tuyß╗ān chß║Ęt th├¼ c├┤ng thß╗®c suy diß╗ģn nhß║źt quyß║┐t ph├ón liß╗ćt biß╗āu thß╗ŗ quy luß║Łt l├┤gic. Ta c├│ thß╗ā kiß╗ām tra qua bß║Żng trß╗ŗ ch├ón l├Į, x├®t trŲ░ß╗Øng hß╗Żp ph├ón liß╗ćt hai th├Ānh phß║¦n (p v q).
| p | q | \(\overline q \) | \(p\underline \vee q\) | \((p\underline \vee q) \wedge p\) | \((p\underline \vee q) \wedge p \to \overline q \) | \((p\underline \vee q) \wedge \overline q \) | \((p\underline \vee q) \wedge \overline q \to \overline p \) |
|
1 1 0 0 |
0 0 1 0 |
0 1 0 1 |
0 1 1 0 |
0 1 0 0 |
1 1 1 1 |
0 1 0 0 |
1 1 1 1 |
C├┤ng thß╗®c hai quy luß║Łt l├┤g├Łe ─æ├│ c├│ thß╗ā sß╗Ł dß╗źng l├Ām quy tß║»c suy diß╗ģn nhß║źt quyß║┐t ph├ón liß╗ćt.
Quy tß║»c khß║│ng ─æß╗ŗnh - phß╗¦ ─æß╗ŗnh (modus ponendo tollens)
\(p\underline \vee q\), p .png) \(\overline q \)
\(\overline q \)
\(p\underline \vee q\), q .png) \(\overline p \)
\(\overline p \)
Quy tß║»c phß╗¦ ─æß╗ŗnh - khß║»ng ─æß╗ŗnh (modus toilens ponendo)
\(p \vee q\), \(\overline p \) .png) q
q
\(p \vee q\), \(\overline q\) .png) p
p
Ngo├Āi ra ─æß╗æi vß╗øi trŲ░ß╗Øng hß╗Żp n├Āy c├│ hai quy tß║»c ├Īp dß╗źng cho ph├®p tuyß║┐n lß╗Ång.
\(p\underline \vee q\), \(\overline p \) .png) q
q
\(p\underline \vee q\), \(\overline q\) .png) p
p
PhŲ░ŲĪng thß╗®c phß╗¦ ─æß╗ŗnh (kh├┤ng ki├¬n thiß║┐t)
Th├Ł dß╗ź:
- Nß║┐u l├Ā h├¼nh thang th├¼ n├│ c├│ bß╗æn cß║Īnh v├Ā c├│ mß╗Öt cß║Ęp cß║Īnh ─æß╗æi song song.
- H├¼nh n├Āy hoß║Ęc kh├┤ng c├│ h├┤n cß║Īnh hoß║Ęc kh├┤ng c├│ cß║Īnh n├Āo song song vß╗øi nhau cß║Ż.
ŌćÆ Vß║Ły h├¼nh n├Āy kh├┤ng phß║Żi h├¼nh thang
H├¼nh thß╗®c logic c├│ dß║Īng:
- \({\rm{p}} \to {\rm{(q}} \wedge {\rm{r)}}\)
- \(\overline q \vee \overline r \)
ŌćÆ Vß║Ły \(\overline p \) hay dß║Īng kh├Īc
(1) \({\rm{[}}p \to (q \wedge r){\rm{]}} \wedge (\overline q \vee \overline r ) \to \overline p \)
(2) \((p \to q) \wedge (p \to r) \wedge (\overline q \vee \overline r ) \to \overline p \)
5. Quy tß║»c suy diß╗ģn
Quy tß║»c suy diß╗ģn ph├ón ra l├Ām hai nh├│m: Quy tß║»c suy diß╗ģn trß╗▒c tiß║┐p v├Ā quy tß║»c suy diß╗ģn gi├Īn tiß║┐p.
C├Īc quy tß║»c suy diß╗ģn trß╗▒c tiß║┐p c├│ ├Į ngh─®a quan trrß╗Źng bao gß╗ōm:
- Modus panens:
.png)
- Modus tollens:
.png)
- Quy tß║»c lß╗▒a chß╗Źn:
.png)
- Quy tß║»c bß║»c cß║¦u:
.png)
C├Īc quy tß║»c suy diß╗ģn gi├Īn tiß║┐p bao gß╗ōm:
Quy tß║»c ─æŲ░a v├Āo ph├Īn ─æo├Īn c├│ ─æiß╗üu kiß╗ćn
.png) trong ─æ├│ T k├Į hiß╗ću tß║Łp hß╗Żp tiß╗ün ─æß╗ü
trong ─æ├│ T k├Į hiß╗ću tß║Łp hß╗Żp tiß╗ün ─æß╗ü
Quy tß║»c dß║½n ─æß║┐n ─æiß╗üu v├┤ l├Į .png)
Quy tß║»c phß║Żn chß╗®ng (xem phß║¦n chß╗®ng minh), thß╗▒c chß║źt l├Ā dß╗▒a tr├¬n lŲ░ß╗Żc ─æß╗ō giß║Ż thuyß║┐t - diß╗ģn dß╗ŗch v├Ā luß║Łt b├Āi trung.











