Nß╗Öi dung b├Āi giß║Żng B├Āi 2: Suy luß║Łn diß╗ģn dß╗ŗch sau ─æ├óy sß║Į gi├║p c├Īc bß║Īn t├¼m hiß╗āu vß╗ü suy diß╗ģn l├Ā g├¼, suy diß╗ģn trß╗▒c tiß║┐p, tam ─æoß║Īn luß║Łn nhß║źt quyß║┐t, suy diß╗ģn gi├Īn tiß║┐p vß╗øi tiß╗ün ─æß╗ü phß╗®c hß╗Żp, quy tß║»c suy diß╗ģn.
T├│m tß║»t l├Į thuyß║┐t
1. Suy diß╗ģn l├Ā g├¼?
Suy diß╗ģn l├Ā loß║Īi suy luß║Łn c├│ hai thuß╗Öc t├Łnh cŲĪ bß║Żn:
- (1) Xuß║źt ph├Īt tß╗½ nhß╗»ng tiß╗ün ─æß╗ü l├Ā nhß╗»ng ph├Īn ─æo├Īn kh├Īi qu├Īt.
- (2) Kß║┐t luß║Łn r├║t ra mß╗Öt c├Īch tß║źt yß║┐u, tß╗®c l├Ā tß║źt suy logic.
Nß║┐u k├Į hiß╗ću tß║źt suy logic l├Ā Ō¢Ī .png) th├¼ h├¼nh thß╗®c logic cß╗¦a suy diß╗ģn c├│ dß║Īng sau ─æ├óy:
th├¼ h├¼nh thß╗®c logic cß╗¦a suy diß╗ģn c├│ dß║Īng sau ─æ├óy:
\(\sum\limits_{i = 1}^n T \)─Éi .png) KL
KL
T├╣y thuß╗Öc sß╗æ lŲ░ß╗Żng tiß╗ün ─æß╗ü ta sß║Į c├│ c├Īc loß║Īi suy diß╗ģn tß╗½ 1 tiß╗ün ─æß╗ü, tß╗½ 2 tiß╗ün ─æß╗ü, tß╗½ 3 tiß╗ün ─æß╗ü, v,v., t├╣y thuß╗Öc t├Łnh chß║źt cß╗¦a ph├Īn ─æo├Īn tiß╗ün ─æß╗ü ta sß║Į c├│ nhß╗»ng loß║Īi suy diß╗ģn nhß║źt quyß║┐t, hay c├│ ─æiß╗üu kiß╗ćn hoß║Ęc c├│ lß╗▒a chß╗Źn, v.v..
2. Suy diß╗ģn trß╗▒c tiß║┐p
Suy diß╗ģn trß╗▒c tiß║┐p l├Ā loß║Īi suy diß╗ģn xuß║źt ph├Īt tß╗½ mß╗Öt tiß╗ün ─æß╗ü, r├║t ra kß║┐t luß║Łn tß╗½ tiß╗ün ─æß╗ü ─æ├│.
H├¼nh thß╗®c logic cß╗¦a suy diß╗ģn trß╗▒c tiß║┐p c├│ dß║Īng:
T─É .png) KL
KL
C├│ nhiß╗üu dß║Īng suy diß╗ģn trß╗▒c tiß║┐p, t├╣y thuß╗Öc c├Īch thß╗®c biß║┐n ─æß╗Ģi ph├Īn ─æo├Īn ti├¬n ─æß╗ü.
TrŲ░ß╗Øng hß╗Żp c├Īc ph├Īn ─æo├Īn tiß╗ün ─æß╗ü l├Ā loß║Īi ph├Īn ─æo├Īn ─æŲĪn, nhß║źt quyß║┐t dß║Īng A,E,O, I trong h├¼nh vu├┤ng logic, ta c├│ thß╗ā c├│ c├Īc dß║Īng suy luß║Łn ─æ├║ng ─æß║»n sau ─æ├óy:
C├│ thß╗ā ─æß╗Ģi chß║źt ph├Īn ─æo├Īn khß║│ng ─æß╗ŗnh th├Ānh phß╗¦ ─æß╗ŗnh hoß║Ęc ngŲ░ß╗Żc lß║Īi.
Th├Ł dß╗ź 1: Mß╗Źi kim loß║Īi ─æß╗üu dß║½n ─æiß╗ćn. (A) = 1
Vß║Ły kh├┤ng c├│ kim loß║Īi n├Āo l├Ā kh├┤ng dß║½n ─æiß╗ćn (E) = 1
Quy tß║»c suy luß║Łn c├│ dß║Īng l├Ā A .png) E, hay l├Ā:
E, hay l├Ā:
\(\frac{{SaM}}{{SeM}}\)
Th├Ł dß╗ź 2: Mß╗Öt sß╗æ thi├¬n nga c├│ m├Āu l├┤ng trß║»ng. (I) = 1
Vß║Ły mß╗Öt sß╗æ thi├¬n nga kh├┤ng c├│ m├Āu l├┤ng trß║»ng. (O) = 1.
Quy tß║»c suy luß║Łn cß╗ź thß╗ā l├Ā: I .png) O hay l├Ā:
O hay l├Ā:
\(\frac{{SiM}}{{SoM}}\)
C├│ thß╗ā ─æß╗Ģi chß╗Ś hay l├Ā ─æß║Żo ngŲ░ß╗Żc chß╗¦ tß╗½ v├Ā vß╗ŗ tß╗½, giß╗» nguy├¬n chß║źt cß╗¦a ph├Īn ─æo├Īn tiß╗ün ─æß╗ü.
Th├Ł dß╗ź 1: Mß╗Öt sß╗æ sinh vi├¬n l├Ā cß║¦u thß╗¦ b├│ng ─æ├Ī. (I) = 1
Vß║Ły mß╗Öt sß╗æ cß║¦u thß╗¦ b├│ng ─æ├Ī l├Ā sinh vi├¬n. (I) = 1
Quy tß║»c suy luß║Łn cß╗ź thß╗ā l├Ā: I .png) I hay l├Ā:
I hay l├Ā:
\(\frac{{SiM}}{{SiM}}\)
Th├Ł dß╗ź 2: Sß╗æ chß║Ąn kh├┤ng l├Ā sß╗æ lß║╗. (E) = 1
Vß║Ły, sß╗æ lß║╗ kh├┤ng l├Ā sß╗æ chß║Ąn. (E) = 1
Quy tß║»c suy luß║Łn c├│ dß║Īng cß╗ź thß╗ā l├Ā E.png) E. hay l├Ā:
E. hay l├Ā:
\(\frac{{SeM}}{{SeM}}\)
C├│ thß╗ā ─æß╗Ģi lŲ░ß╗Żng ph├Īn ─æo├Īn chung th├Ānh ph├Īn ─æo├Īn ri├¬ng.
Th├Ł dß╗ź 1: Mß╗Źi kim loß║Īi ─æß╗üu dß║½n diß╗ćn. (A) = 1
Vß║Ły, mß╗Öt sß╗æ kim loß║Īi dß║½n ─æiß╗ćn. (I) = 1
Quy tß║»c suy luß║Łn c├│ dß║Īng cß╗ź thß╗ā l├Ā: A .png) I, hay l├Ā:
I, hay l├Ā:
\(\frac{{SaM}}{{SiM}}\)
Th├Ł dß╗ź 2: Mß╗Źi kß║╗ xu nß╗ŗnh ─æß╗üu kh├┤ng c├│ l├▓ng tß╗▒ trß╗Źng. (E) = 1
Vß║Ły, mß╗Öt sß╗æ kß║╗ xu nß╗ŗnh kh├┤ng c├│ tß╗▒ trß╗Źng. (O) = 1
Quy tß║»c suy luß║Łn c├│ dß║Īng cß╗ź thß╗ā l├Ā: E.png) O, hay l├Ā:
O, hay l├Ā:
\(\frac{{SeM}}{{SoM}}\)
Hai dß║Īng suy luß║Łn ─æ├║ng ─æß║»n n├Āy ─æß╗üu dß╗▒a tr├¬n cung mß╗Öt quy tß║»c logic chung, (thŲ░ß╗Øng ─æŲ░ß╗Żc gß╗Źi l├Ā c├┤ng l├Į): nß║┐u tiß╗ün ─æß╗ü l├Ā ph├Īn ─æo├Īn chung ch├ón thß╗▒c thi tß║źt yß║┐u suy ra kß║┐t luß║Łn l├Ā ph├Īn ─æo├Īn ri├¬ng c┼®ng ch├ón thß╗▒c. N├│i c├Īch kh├Īc, nß║┐u ─æ├║ng cho to├Ān thß╗ā th├¼ tß║źt nhi├¬n l├Ā ─æ├║ng cho bß╗Ö phß║Łn. Trong logic vß╗ŗ Lß╗½, quy tß║»c logic chung n├¬u tr├¬n c├│ dß║Īng h├¼nh thß╗®c h├│a sau ─æ├óy:
\(\frac{{(\forall x)P(x)}}{{P(a)}}\)
Ch├║ ├Į, c├│ thß╗ā kß║┐t luß║Łn l├Ā ch├ón thß╗▒c nhŲ░ng tiß╗ün dß╗ü l├Ā giß║Ż ─æß╗æi. ─É├│ l├Ā trŲ░ß╗Øng hß╗Żp suy luß║Łn theo luß║Łt b├Āi trung:
\((\forall x)(x \vee \overline x ) \equiv 1\)
TrŲ░ß╗Øng hß╗Żp thß╗® nhß║źt, A giß║Ż ─æß╗æi suy ra O ch├ón thß╗▒c v├Ā ngŲ░ß╗Żc lß║Īi.
Th├Ł dß╗ź 1: Mß╗Źi thi├¬n nga ─æß╗üu l├┤ng trß║»ng. (A) = 0
Vß║Ły, mß╗Öt sß╗æ thi├¬n nga l├┤ng kh├┤ng trß║»ng. (O) = 1
TrŲ░ß╗Øng hß╗Żp thß╗® hai, E giß║Ż dß╗æi suy ra I ch├ón thß╗▒c v├Ā ngŲ░ß╗Żc lß║Īi.
Th├Ł dß╗ź 2: Mß╗Źi ngŲ░ß╗Øi ─æau ß╗æm ─æß╗üu kh├┤ng ─æŲ░ß╗Żc khen thŲ░ß╗¤ng. (E) = 0
Vß║Ły, mß╗Öt sß╗æ ngŲ░ß╗Øi ─æau ├┤m ─æŲ░ß╗Żc khen thŲ░ß╗¤ng. (I) = 1
Ph├Īn ─æo├Īn tiß╗ün ─æß╗ü c├│ thß╗ā l├Ā ph├Īn ─æo├Īn phß╗®c hß╗Żp, khi ─æ├│ kß║┐t luß║Łn bß║▒ng tß║źt suy logic c├│ thß║┐ thu ─æŲ░ß╗Żc bß║▒ng c├Īch biß║┐n ─æß╗Ģi ─æß╗ōng nhß║źt thß╗®c.
Chß║│ng hß║Īn,
- Tiß╗ün ─æß╗ü: Nß║┐u trß╗Øi mŲ░a th├¼ ─æŲ░ß╗Øng Ų░ß╗øt.
- Kß║┐t luß║Łn: Vß║Ły, nß║┐u ─æŲ░ß╗Øng kh├┤ng Ų░ß╗øt th├¼ trß╗Øi kh├┤ng mŲ░a.
Quy tß║»c kß║┐t luß║Łn c├│ dß║Īng chung l├Ā:
\((P \to Q)\) .png) \((\overline Q \to \overline P )\) hay l├Ā \(\frac{{P \to Q}}{{(\overline Q \to \overline P )}}\)
\((\overline Q \to \overline P )\) hay l├Ā \(\frac{{P \to Q}}{{(\overline Q \to \overline P )}}\)
NhŲ░ ─æ├Ż biß║┐t, quy tß║»c De Morgan c├│ hai hß╗ć thß╗®c:
(1) \(\overline {P \wedge Q} = \overline P \vee \overline Q \)
(2) \(\overline {P \vee Q} = \overline P \wedge \overline Q \)
Tß╗½ ─æ├│, tŲ░ŲĪng ß╗®ng vß╗øi ch├║ng, ta c├│ nguy├¬n tß║»c suy luß║Łn trß╗▒c tiß║┐p sau ─æ├óy:
(1a) \(\frac{{\overline {P \wedge Q} }}{{\overline P \vee \overline Q }};\,\,\,\,\,\,\,\,\,\,\frac{{\overline P \vee \overline Q }}{{\overline {P \wedge Q} }}\)
(2a) \( \frac{{\overline {P \vee Q} }}{{\overline P \wedge \overline Q }};\,\,\,\,\,\,\,\,\,\,\frac{{\overline P \wedge \overline Q }}{{\overline {P \vee Q} }}\)
3. Tam ─æoß║Īn luß║Łn nhß║źt quyß║┐t
3.1 Tam ─æoan luß║Łn nhß║źt quyß║┐t l├Ā g├¼
TrŲ░ß╗Øng hß╗Żp ─æŲĪn giß║Żn nhß║źt l├Ā suy diß╗ģn tß╗½ hai tiß╗ün ─æß╗ü. Nß║┐u tiß╗ün ─æß╗ü l├Ā c├Īc ph├Īn ─æo├Īn ─æŲĪn, nhß║źt quyß║┐t dß║Īng A, E, O, I th├¼ ngŲ░ß╗Øi ta gß╗Źi l├Ā tam ─æoß║Īn luß║Łn nhß║źt quyß║┐t.
Th├Ł dß╗ź:
Mß╗Źi kim loß║Īi ─æß╗üu dß║½n ─æiß╗ćn.
─Éß╗ōng l├Ā kim loß║Īi.
ŌćÆ Vß║Ły, ─æß╗ōng l├Ā chß║źt dß║½n ─æiß╗ćn.
3.2 Cß║źu tr├║c cß╗¦a tam ─æoan luß║Łn nhß║źt quyß║┐t
- Cß║źu tr├║c cß╗¦a tam ─æoß║Īn luß║Łn nhß║źt quyß║┐t bao gß╗ōm hai tiß╗ün ─æß╗ü, ─æß╗®ng trŲ░ß╗øc l├Ā ─æß║Īi tiß╗ün ─æß╗ü (tiß╗ün ─æß╗ü lß╗øn), ─æß╗®ng sau gß╗Źi l├Ā tiß╗āu tiß╗ün ─æß╗ü (tiß╗ün ─æß╗ü nhß╗Å), mß╗Öt kß║┐t luß║Łn. Qu├Ī tr├¼nh ─æi tß╗½ tiß╗ün dß╗ā ─æß║┐n kß║┐t luß║Łn l├Ā tß║źt suy l├┤gic.
- Chß╗¦ tß╗½ (S) trong c├óu kß║┐t luß║Łn gß╗Źi l├Ā tiß╗āu tß╗½ (thuß║Łt ngß╗» nhß╗Å), vß╗ŗ tß╗½ (P) cß╗¦a n├│ gß╗Źi l├Ā ─æß║Īi tß╗½ (thuß║Łt ngß╗» lß╗øn), c├▓n trung tß╗½ (thuß║Łt ngß╗» giß╗»a), k├Į hiß╗ću l├Ā M, c├│ mß║Ęt trong cß║Ż hai tiß╗ün ─æß╗ü lß╗øn v├Ā nhß╗Å.
3.3 Ph├ón loß║Īi tam ─æoß║Īn luß║Łn nhß║źt quyß║┐t
T├╣y thuß╗Öc v├Āo vß╗ŗ tr├Ł cß╗¦a trung tß╗½ m├Ā ta c├│ 4 loß║Īi h├¼nh tam ─æoß║Īn luß║Łn kh├Īc nhau:
Loß║Īi h├¼nh 1:
Th├Ł dß╗ź:
Mß╗Źi sinh vß║Łt (M) ─æß╗āu c├│ t├Łnh di truyß╗ün. (P)
M├©o (S) l├Ā sinh vß║Łt. (M)
ŌćÆ Vß║Ły M├©o (S) c├│ t├Łnh di truyß╗ün, (P)
Loß║Īi h├¼nh 2:

Th├Ł dß╗ź:
Mß╗Źi suy luß║Łn ─æ├║ng (P) ─æß╗üu c├│ sß╗®c thuyß║┐t phß╗źc (M)
Kh├┤ng mß╗Öt sß╗▒ ngß╗źy biß╗ćn n├Āo (S) c├│ sß╗®c thuyß║┐t phß╗źc (M)
ŌćÆ Vß║Ły kh├┤ng mß╗Öt sß╗▒ ngß╗źy biß╗ćn n├Āo (S) l├Ā suy luß║Łn ─æ├║ng (P)
Loß║Īi h├¼nh 3:

Th├Ł dß╗ź:
Mß╗Źi ngŲ░ß╗Øi (M) ─æß╗üu muß╗æn sß╗æng hß║Īnh ph├║c. (P)
Mß╗Źi ngŲ░ß╗Øi (M) ─æß╗üu ham hiß╗āu biß║┐t. (S)
ŌćÆ Vß║Ły, c├│ nhß╗»ng ngŲ░├▓i ham hiß╗āu biß║┐t (S), muß╗æn sß╗æng hß║Īnh ph├║c (P)
Loß║Īi h├¼nh 4:
Th├Ł dß╗ź:
C├│ vß║Łn ─æß╗Öng vi├¬n (P) l├Ā cß║¦u thß╗¦ b├│ng ─æ├Ī. (M)
Cß║¦u thß╗¦ b├│ng ─æ├Ī (M) phß║Żi c├│ sß╗®c khß╗Åe. (S)
ŌćÆ Vß║Ły mß╗Öt sß╗æ ngŲ░ß╗Øi c├│ sß╗®c khß╗Åe (S) l├Ā vß║Łn ─æß╗Öng vi├¬n. (P)
Trong mß╗Śi loß║Īi h├¼nh tam ─æoß║Īn luß║Łn c├│ mß╗Öt sß╗æ kiß╗āu (hay c├Īch) kß║┐t hß╗Żp c├Īc ph├Īn ─æo├Īn A, E, O, I. C├│ 4 loß║Īi ph├Īn ─æo├Īn A, E, O, I. Mß╗Śi tam ─æoß║Īn luß║Łn c├│ 3 ph├Īn ─æo├Īn, vß║Ły ta sß║Į c├│ 44= 64 c├Īch tß║źt cß║Ż. Sß╗æ c├Īch khß║Ż d─® tß╗æi ─æa cho cß║Ż 4 loß║Īi h├¼nh sß║Į l├Ā: 64 x 4 = 256
Sau khi loß║Īi bß╗Å nhß╗»ng c├Īch phi l├Į, kiß╗āu nhŲ░ EEA (tß╗½ hai tiß╗ān ─æß╗ü phß╗¦ ─æß╗ŗnh suy ra kß║┐t luß║Łn khß║│ng ─æß╗ŗnh l├Ā kh├┤ng thß╗ā ─æŲ░ß╗Żc), hay nhŲ░ IAO (tß╗½ hai tiß╗ün ─æß╗ü khß║│ng ─æß╗ŗnh kh├┤ng thß╗ā r├║t ra kß║┐t luß║Łn phß╗¦ ─æß╗ŗnh), c├▓n lß║Īi 19 c├Īch hß╗Żp l├Į.
3.4 C├┤ng l├Į v├Ā quy tß║»c tam ─æoan luß║Łn
C├Īc c├┤ng l├Į:
Mß╗Źi tam ─æoß║Īn luß║Łn ─æ├║ng ─æß║»n ─æß╗üu dß╗▒a v├Āo hai c├┤ng l├Į sau ─æ├óy:
Khß║│ng ─æß╗ŗnh to├Ān bß╗Ö c├│ ngh─®a l├Ā khß║│ng ─æß╗ŗnh bß╗Ö phß║Łn.
\(\frac{{(\forall x)P(x)}}{{(\exists x)P(x)}}\)
TŲ░ŲĪng ß╗®ng vß╗øi n├│ l├Ā: phß╗¦ ─æß╗ŗnh to├Ān bß╗Ö c├│ ngh─®a l├Ā phß╗¦ ─æß╗ŗnh bß╗Ö phß║Łn
\(\frac{{(\forall x)\overline {P(x)} }}{{(\exists x)\overline {P(x)} }}\)
Thuß╗Öc t├Łnh cß╗¦a thuß╗Öc t├Łnh cß╗¦a sß╗▒ vß║Łt, hiß╗ćn tŲ░ß╗Żng l├Ā thuß╗Öc t├Łnh cß╗¦a bß║Żn th├ón sß╗▒ vß║Łt, hiß╗ćn tŲ░ß╗Żng.
Th├Ł dß╗ź:
Mß╗Źi sinh vß║Łt (M) ─æß╗üu c├│ t├Łnh di truyß╗ün. (P)
NgŲ░ß╗Øi (S) l├Ā sinh vß║Łt. (M)
ŌćÆ Vß║Ły ngŲ░ß╗Øi (S) c├│ t├Łnh di truyß╗ün (P)
C├Īc quy tß║»c:
Ngo├Āi c├┤ng l├Į, c├▓n c├│ nhiß╗üu quy tß║»c tam ─æoß║Īn luß║Łn. Ch├║ng ─æŲ░ß╗Żc ph├ón ra th├Ānh hai nh├│m lß╗øn. Nh├│m thß╗® nhß║źt l├Ā quy tß║»c chung cho cß║Ż 4 loß║Īi h├¼nh v├Ā nh├│m thß╗® hai l├Ā quy tß║»c ri├¬ng cß╗¦a mß╗æi loß║Īi h├¼nh tam ─æoß║Īn luß║Łn.
* Nh├│m, quy tß║»c chung cho cß║Ż 4 loß║Īi h├¼nh tam ─æoß║Īn luß║Łn bao gß╗ōm:
- C├Īc quy tß║»c ─æß╗æi vß╗øi thuß║Łt ngß╗»
Quy tß║»c 1: Trong mß╗Öt tam ─æoß║Īn luß║Łn chß╗ē c├│ ba thuß║Łt ngß╗» (S), (P) v├Ā (M). Nß║┐u c├│ thuß║Łt ngß╗» thß╗® tŲ░, th├¼ ngŲ░ß╗Øi ta gß╗Źi l├Ā "sai lß║¦m bß╗æn thuß║Łt ngß╗»".
Th├Ł dß╗ź:
Vß║Łn ─æß╗Öng (M) l├Ā v─®nh cß╗Łu. (P)
─Éi l├Ām (S) l├Ā vß║Łn ─æß╗Öng. (M)
ŌćÆ Vß║Ły ─æi l├Ām (S) l├Ā v─®nh cß╗Łu. (P)
R├Ą r├Āng c├óu kß║┐t luß║Łn rß║źt phi l├Į v├Ā nguy├¬n nh├ón sß╗▒ phi l├Į ─æ├│ l├Ā ngŲ░ß╗Øi lß║Łp luß║Łn mß║»c lß╗Śi 4 thuß║Łt ngß╗», thuß║Łt ngß╗» "vß║Łn ─æß╗Öng" trong ─æß║Īi tiß╗ün ─æß╗ü v├Ā trong tiß╗āu tiß╗ün ─æß╗ü l├Ā hai kh├Īi niß╗ćm kh├Īc nhau; vß║Łn ─æß╗Öng trong ─æß║Īi tiß╗üu ─æß╗ü l├Ā ─æß║Ęc t├Łnh phß╗Ģ biß║┐n cß╗¦a mß╗Źi sß╗▒ vß║Łt, hiß╗ćn tŲ░ß╗Żng, c├▓n vß║Łn ─æß╗Öng trong tiß╗āu tiß╗ün ─æß╗ü l├Ā h├Ānh ─æß╗Öng cß╗ź thß╗ā cß╗¦a con ngŲ░ß╗Øi.
Quy tß║»c 2: Trung tß╗½ (M) phß║Żi chu di├¬n (tß╗®c l├Ā c├│ ngoß║Īi di├¬n ─æß║¦y ─æß╗¦) ├Łt nhß║źt mß╗Öt lß║¦n. Nß║┐u vi phß║Īm quy tß║»c n├Āy th├¼ kß║┐t luß║Łn kh├┤ng tß║źt suy l├┤gic tß╗½ hai tiß╗ün ─æß╗ü ─æ├Ż cho.
Th├Ł dß╗ź:
Kim loß║Īi (P) dß║½n ─æiß╗ćn. (M)
─Éß╗ōng (S) dß║½n ─æiß╗ćn. (M)
Suy luß║Łn tr├¬n kh├┤ng thß╗ā r├║t ra kß║┐t luß║Łn, bß╗¤i v├¼ trung tß╗½ "dß║½n ─æiß╗ćn" kh├┤ng chu di├¬n ├Łt nhß║źt mß╗Öt lß║¦n. Ta c├│ thß╗ā ngh─® rß║▒ng ph├Īn ─æo├Īn "─Éß╗ōng l├Ā kim loß║Īi" l├Ā tß║źt suy l├┤gic tß╗½ hai tiß╗ün ─æß╗ü n├¬u tr├¬n, nhŲ░ng thß╗▒c ra ph├Īn ─æo├Īn ─æ├│ l├Ā ch├ón thß╗▒c ─æß╗Öc lß║Łp vß╗øi hai tiß╗ün ─æß╗ü d├Ż cho.
Ta sß║Į thß║źy r├Ą hŲĪn trong trŲ░ß╗Øng hß╗Żp tam ─æoß║Īn luß║Łn cß╗ź thß╗ā sau ─æ├óy:
M├©o (P) ─ān chuß╗Öt. (M)
NgŲ░ß╗Øi (S) ─ān chuß╗Öt. (M)
ŌćÆ Vß║Ły, ngŲ░ß╗Øi (S) l├Ā m├©o (P)
Quy tß║»c 3: Thuß║Łt ngß╗» n├Āo kh├┤ng chu di├¬n trong tiß╗ün ─æß╗ü th├¼ c┼®ng kh├┤ng thß╗ā chu di├¬n trong kß║┐t luß║Łn.
Th├Ł dß╗ź:
L├Ām thŲĪ (M) l├Ā hoß║Īt ─æß╗Öng nghß╗ć thuß║Łt. (P)
L├Ām thŲĪ (M) c┼®ng l├Ā lao ─æß╗Öng. (S)
ŌćÆ Vß║Ły, mß╗Źi lao ─æß╗Öng l├Ā hoß║Īt ─æß╗Öng nghß╗ć thuß║Łt,
Ta kh├┤ng thß╗ā r├║t ra kß║┐t luß║Łn "mß╗Źi lao ─æß╗Öng ─æß╗üu l├Ā hoß║Īt ─æß╗Öng nghß╗ć thuß║Łt", v├¼ trong kß║┐t luß║Łn n├Āy chß╗¦ tß╗½ "lao ─æß╗Öng" l├Ā chu di├¬n trong khi ─æ├│ trong tiß╗ün ─æß╗ü nhß╗Å, vß╗ŗ tß╗½ lao ─æß╗Öng kh├┤ng chu di├¬n, tß╗½ t├Łnh bß║źt ─æß╗ŗnh c├│ trong tiß╗ün dß╗ü kh├┤ng thß╗ā tß║źt suy ra t├Łnh tß║źt ─æß╗ŗnh trong kß║┐t luß║Łn ─æŲ░ß╗Żc. NhŲ░ng ta ho├Ān to├Ān c├│ thß╗ā r├║t ra kß║┐t luß║Łn hß╗Żp logic nhŲ░ sau: "Mß╗Öt sß╗æ lao ─æß╗Öng l├Ā hoß║Īt ─æß╗Öng nghß╗ć thuß║Łt". C├óu kß║┐t luß║Łn l├Ā ch├ón thß╗▒c v├Ā ─æŲ░ß╗Żc tß║źt suy logic tß╗½ hai tiß╗ün ─æß╗ü ─æ├Ż cho.
- Quy tß║»c ─æß╗æi vß╗øi tiß╗ün ─æß╗ü
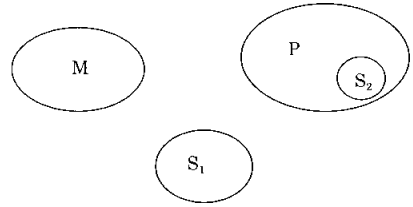
Quy tß║»c 1: Tß╗½ hai tiß╗ün ─æß╗ü l├Ā ph├Īn ─æo├Īn phß╗¦ ─æß╗ŗnh kh├┤ng thß╗ā r├║t ─æŲ░ß╗Żc kß║┐t luß║Łn g├¼.
Th├Ł dß╗ź:
Mß╗Źi hß╗Źc sinh tiß╗āu hß╗Źc (M) ─æß╗üu kh├┤ng m├╣ chß╗» (P)
Chß╗ŗ Nga (S) kh├┤ng phß║Żi l├Ā hß╗Źc sinh tiß╗āu hß╗Źc (M)
ŌćÆ Vß║Ły kh├┤ng thß╗ā kß║┐t luß║Łn tß║źt suy logic.
Bß║▒ng sß╗Ø ─æß╗ō Gi.Ven ta thß║źy r├Ą giß╗»a (S) v├Ā (P) kh├┤ng c├│ mß╗æi li├¬n hß╗ć tß║źt ─æß╗ŗnh, cho n├¬n kh├┤ng thß╗ā suy ra kß║┐t luß║Łn tß║źt suy logic:
Quy tß║»c 2: Tß╗½ hai tiß╗ün ─æß╗ü l├Ā ph├Īn ─æo├Īn ri├¬ng kh├┤ng thß╗ā r├║t ra kß║┐t luß║Łn g├¼
Th├Ł dß╗ź:
Mß╗Öt sß╗æ thi├¬n nga (M) c├│ l├┤ng m├Āu ─æen. (P)
Một số thiên nga (M) đẹp. (S)
ŌćÆ Vß║Ły, kh├┤ng thß╗ā r├║t ra kß║┐t luß║Łn "mß╗Öt sß╗æ thi├¬n nga ─æß║╣p (S) c├│ l├┤ng m├Āu ─æen (p)", bß╗¤i v├¼ nhŲ░ thß║┐ sß║Į vi phß║Īm quy tß║»c 2 ─æß╗æi vß╗øi thuß║Łt ngß╗»: Thuß║Łt ngß╗» (M) kh├┤ng chu di├¬n trong cß║Ż hai tiß╗ün dß╗ü.
Quy tß║»c 3: Tß╗½ hai tiß╗ün ─æß╗ü khß║│ng ─æß╗ŗnh kh├┤ng thß╗ā r├║t ra kß║┐t luß║Łn phß╗¦ ─æß╗ŗnh.
Th├Ł dß╗ź:
Tß║źt cß║Ż c├Īc g├│c tr├¬n ─æŲ░ß╗Øng k├Łnh (M) cß╗¦a mß╗Öt v├▓ng tr├▓n ─æß╗üu l├Ā g├│c vu├┤ng (P).
G├│c nß╗Öi tiß║┐p d├Ż cho (S) tr├¬n ─æŲ░ß╗Øng k├Łnh (M).
ŌćÆ Vß║Ły, chß╗ē c├│ kß║┐t luß║Łn rß║▒ng g├│c nß╗Öi tiß║┐p ─æ├Ż cho (S) l├Ā g├│c vu├┤ng. (P)
Quy tß║»c 4: Nß║┐u c├│ mß╗Öt tiß╗ün ─æß╗ü ri├¬ng, th├¼ kh├┤ng thß╗ā r├║t ra kß║┐t luß║Łn chung
Th├Ł dß╗ź:
Mß╗Źi C├Īcbon Hydro (M) ─æß╗üu l├Ā hß╗Żp chß║źt hß╗»u cŲĪ. (P)
Mß╗Öt sß╗æ C├Īcbon Hydro (M) l├Ā chß║źt kh├Ł. (S)
ŌćÆ Vß║Ły, mß╗Öt sß╗æ chß║źt kh├Ł (S) l├Ā hß╗Żp chß║źt hß╗»u cŲĪ. (P)
Quy tß║»c 5: Nß║┐u c├│ mß╗Öt tiß╗ün ─æß╗ü phß╗¦ ─æß╗ŗnh th├¼ kh├┤ng thß╗ā c├│ kß║┐t luß║Łn khß║»ng ─æß╗ŗnh.
Th├Ł dß╗ź:
Mß╗Źi suy luß║Łn ─æ├║ng (P) ─æß╗üu c├│ sß╗®c thuyß║┐t phß╗źc. (M)
Kh├┤ng mß╗Öt sß╗▒ ngß╗źy biß╗ćn n├Āo (S) c├│ sß╗®c thuyß║┐t phß╗źc. (M)
ŌćÆ Vß║Ły, kh├┤ng c├│ sß╗▒ ngß╗źy biß╗ćn n├Āo (S) l├Ā suy luß║Łn ─æ├║ng. (P)
Nh├│m quy tß║»c ri├¬ng cß╗¦a c├Īc loß║Īi h├¼nh tam ─æoß║Īn luß║Łn bao gß╗ōm:
- Quy tß║»c cß╗¦a loß║Īi h├¼nh 1
- Tiß╗ün ─æß╗ü lß╗øn phß║Żi l├Ā ph├Īn ─æo├Īn chung;
- Tiß╗ün ─æß╗ü nhß╗Å phß║Żi l├Ā ph├Īn ─æo├Īn khß║│ng ─æß╗ŗnh.
- C├Īc c├Īch hß╗Żp l├┤g├Łc cß╗¦a loß║Īi h├¼nh 1 l├Ā:
- bArbArA, viß║┐t tß║»t l├Ā AAA
- cElArEnt. viß║┐t tß║»t l├Ā EAE
- dArII, viß║┐t tß║»t l├Ā AII
- fErIO, viß║┐t tß║»t l├Ā EIO
- Quy tß║»c cß╗¦a loß║Īi h├¼nh 2
- Tiß╗ün ─æß╗ü lß╗øn phß║Żi l├Ā ph├Īn ─æo├Īn chung;
- Mß╗Öt trong hai tiß╗ün ─æß╗ü phß║Żi l├Ā ph├Īn ─æo├Īn phß╗¦ ─æß╗ŗnh.
- C├Īc c├Īch hß╗▒p l├┤gic cß╗¦a loß║Īi h├¼nh 2 l├Ā:
- cEsArE viß║┐t tß║»t l├Ā EAE
- cAmEstrEs viß║┐t tß║»t l├Ā AEE
- fEstlnO viß║┐t tß║»t l├Ā EIO
- bArOcO viß║┐t tß║»t l├Ā AOO
- Quy tß║»c cß╗¦a loß║Īi h├¼nh 3
- Tiß╗ün ─æß╗ü nhß╗Å phß║Żi l├Ā khß║│ng ─æß╗ŗnh;
- Kß║┐t luß║Łn phß║Żi l├Ā ph├Īn ─æo├Īn ri├¬ng.
- C├Īc c├Īch hß╗Żp l├┤gic cß╗¦a loß║Īi h├¼nh 3 l├Ā:
- dArAptI viß║┐t tß║»t l├Ā AAI
- dlsAmIs viß║┐t tß║»t l├Ā IAI
- dAtIsI viß║┐t tß║»t l├Ā AII
- fELAptOn viß║┐t tß║»t l├Ā EAO
- bOkArdO viß║┐t tß║»t l├Ā OAO
- fErIsOn viß║┐t tß║»t l├Ā EIO
- Quy tß║»c cß╗¦a loß║Īi h├¼nh 4
- Tiß╗ün ─æß╗ā kh├┤ng ─æŲ░ß╗Żc l├Ā ph├Īn ─æo├Īn phß╗¦ ─æß╗ŗnh ri├¬ng;
- Kß║┐t luß║Łn kh├┤ng bao giß╗Ø l├Ā khß║│ng ─æß╗ŗnh chung.
- C├Īc c├Īch hß╗Żp logic cß╗¦a loß║Īi h├¼nh 4 l├Ā:
- brAmAntdp viß║┐t tß║»t l├Ā AAI
- cAmEnEs vi├¬l tß║»t l├Ā AEE
- dImArIs viß║┐t tß║»t l├Ā IAI
- fEsApO viß║┐t tß║»t l├Ā EAO
- frEsIsOn vied tß║»t l├Ā EIO
Mß╗Öt sß╗æ dß║Īng ─æß║Ęc biß╗ćt cß╗¦a tam ─æoß║Īn luß║Łn nhß║źt quyß║┐t
Luß║Łn hai ─æoß║Īn thß╗▒c chß║źt l├Ā tam ─æoß║Īn luß║Łn r├║t gß╗Źn hay c├▓n gß╗Źi l├Ā tam ─æoß║Īn luß║Łn tß╗ēnh lŲ░ß╗Żc.
Th├Ł dß╗ź:
"X├┤cr├Īt l├Ā ngŲ░ß╗Øi, X├┤cr├Īt ─æ├Ż chß║┐t".
─É├óy l├Ā luß║Łn hai ─æoß║Īn, nhŲ░ng thß╗▒c chß║źt l├Ā dß║Īng r├║t gß╗Źn cß╗Ła luß║Łn ba ─æoß║Īn. Nß║┐u kh├┤i phß╗źc lß║Īi ta thß║źy nhŲ░ sau:
Mß╗Źi ngŲ░ß╗Øi (M) ─æß╗üu phß║Żi chß║┐t. (P)
X├┤cr├Īt (S) l├Ā ngŲ░ß╗Øi. (M)
ŌćÆ Vß║Ły, X├┤cr├Īt (S) phß║Żi chß║┐t. (P)
Ngh─®a l├Ā ß╗¤ ─æ├óy, tiß╗ün ─æß╗ü lß╗øn ─æ├Ż bß╗ŗ lŲ░ß╗Żc bß╗Å ─æi.
C┼®ng c├│ thß╗ā lŲ░ß╗Żc bß╗Å ─æi tiß╗ün ─æß╗ü nhß╗Å, chß║│ng hß║Īn nhŲ░ "─É├Ż l├Ā ngŲ░ß╗Øi th├¼ phß║Żi chß║┐t, vß║Ły X├┤cr├Īl phß║Żi chß║┐t" Hoß║Ęc c├│ thß╗ā lŲ░ß╗Żc bß╗Å kß║┐t luß║Łn:
Th├Ł dß╗ź:
"Mß╗Źi ngŲ░ß╗Øi ─æß╗üu phß║Żi chß║┐t, X├┤cr├Īt c┼®ng l├Ā ngŲ░ß╗Øi kia m├Ā".
Tam ─æoß║Īn luß║Łn phß╗®c hß╗Żp thß╗▒c chß║źt l├Ā li├¬n kß║┐t nhiß╗üu tam ─æoß║Īn luß║Łn ─æß╗ā cuß╗æi c├╣ng r├║t ra mß╗Öt kß║┐t luß║Łn chung.
C├│ thß╗ā li├¬n kß║┐t theo kiß╗āu d├╣ng kß║┐t luß║Łn cß╗¦a tam ─æoß║Īn luß║Łn ─æß╗®ng trŲ░ß╗øc l├Ām tiß╗ün ─æß╗ü cho tam ─æoß║Īn luß║Łn ─æß╗®ng sau.
Th├Ł dß╗ź:
Mß╗Źi sinh vß║Łt ─æß╗üu trao ─æß╗æi chß║źt.
Mß╗Źi ─æß╗Öng vß║Łt ─æß╗üu l├Ā sinh vß║Łt.
Vß║Ły mß╗Źi ─æß╗Öng vß║Łt ─æß╗üu trao ─æß╗æi chß║źt.
Mß╗Źi giß╗æng m├©o ─æß╗üu l├Ā ─æß╗Öng vß║Łt.
ŌćÆ Vß║Ły mß╗Źi giß╗æng m├©o ─æß╗üu trao ─æß╗Ģi chß║źt.
DŲ░ß╗øi dß║Īng r├║t gß╗Źn ta c├│:
Mß╗Źi sinh vß║Łt ─æß╗üu trao ─æß╗Ģi chß║źt.
Mß╗Źi ─æß╗Öng vß║Łt ─æß╗üu l├Ā sinh vß║Łt.
Mß╗Źi giß╗æng m├©o ─æß╗üu l├Ā ─æß╗Öng vß║Łt.
ŌćÆ Vß║Ły mß╗Źi giß╗æng m├©o ─æß╗üu trao ─æß╗Ģi chß║źt,
Dß║Īng r├║t gß╗Źn n├Āy cß╗¦a tam ─æoß║Īn luß║Łn phß╗®c hß╗Żp gß╗Źi l├Ā luß║Łn ti├¬u kß║┐t Goklen. Thß╗▒c chß║źt luß║Łn li├¬n kß║┐t Goklen l├Ā tam ─æoß║Īn luß║Łn phß╗®c hß╗Żp lŲ░ß╗Żc bß╗Å tiß╗ün ─æß╗ü lß╗øn.
H├¼nh thß╗®c logic cß╗¦a luß║Łn ti├¬u1 kß║┐t Goklen c├│ dß║Īng sau ─æ├óy:
P1 l├Ā P
P2 l├Ā P1
P3 l├Ā P2
ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”.
Pn l├Ā Pn-1
S l├Ā Pn
ŌćÆ Vß║Ły, S l├Ā P
NhŲ░ vß║Ły l├Ā trong luß║Łn ti├¬u kß║┐t Goklen, ngŲ░ß╗Øi ta lß║źy chß╗¦ tß╗½ cß╗¦a tiß╗ün ─æß╗ü trŲ░ß╗øc l├Ām vß╗ŗ tß╗½ cß╗¦a tiß╗ün ─æß╗ü sau v├Ā cß╗® thß║┐ tiß║┐p tß╗źc. Cuß╗æi c├╣ng lß║źy chß╗¦ tß╗½ cß╗¦a tiß╗ün ─æß╗ā sau c├╣ng hß╗Żp vß╗øi vß╗ŗ tß╗½ cß╗¦a tiß╗ün ─æß╗ü ─æß║¦u ti├¬n l├Ām th├Ānh kß║┐t luß║Łn.
Luß║Łn ti├¬u kß║┐t Arixtß╗æt th├¼ c├│ dß║Īng kh├Īc hß║│n vß╗øi luß║Łn ti├¬u kß║┐t Goklen. N├│ giß║Żn lŲ░ß╗Żc tiß╗ün ─æß╗ü nhß╗Å, bß║▒ng c├Īch lß║źy vß╗ŗ tß╗½ cß╗¦a tiß╗ün ─æß╗ā trŲ░ß╗øc l├Ām chß╗¦ tß╗½ cß╗¦a tiß╗ün dß╗ü sau. Cuß╗æi c├╣ng lß║źy chß╗¦ tß╗½ cß╗¦a tiß╗ün ─æß╗ü ─æß║¦u ti├¬n hß╗Żp vß╗øi vß╗ŗ tß╗½ cß╗¦a tiß╗ün ─æß╗ü sau c├╣ng ─æß╗ā l├Ām th├Ānh kß║┐t luß║Łn.
Th├Ł dß╗ź:
- Sß╗æ 3 l├Ā sß╗æ lß║╗.
- Mß╗Źi sß╗æ lß║╗ ─æß╗üu l├Ā sß╗æ tß╗▒ nhi├¬n.
- Mß╗Źi sß╗æ tß╗▒ nhi├¬n ─æß╗üu l├Ā sß╗æ hß╗»u tß╗Ę.
- Mß╗Źi sß╗æ hß╗»u tß╗Ę ─æß╗üu l├Ā sß╗æ thß╗▒c.
ŌćÆ Vß║Ły, sß╗æ 3 l├Ā sß╗æ thß╗▒c.
Nß║┐u kh├┤i phß╗źc tiß╗ün ─æß╗ü nhß╗Å ─æ├Ż bß╗ŗ lŲ░ß╗Żc bß╗Å th├¼ ta sß║Į c├│ dß║Īng ─æß║¦y ─æß╗¦ nhŲ░ sau:
- Mß╗Źi sß╗æ lß║╗ ─æß╗üu l├Ā sß╗æ tß╗▒ nhi├¬n.
- Sß╗æ 3 l├Ā sß╗æ lß║╗.
- Vß║Ły, sß╗æ 3 l├Ā sß╗æ tß╗▒ nhi├¬n.
- Mß╗Źi sß╗æ tß╗▒ nhi├¬n ─æß╗üu l├Ā sß╗æ hß╗»u tß╗Ę (sß╗æ 3 l├Ā sß╗æ tß╗▒ nhi├¬n)
ŌćÆVß║Ły, sß╗æ 3 l├Ā sß╗æ hß╗»u t├Į.
- Mß╗Źi sß╗æ hß╗»u tß╗Ę ─æß╗üu l├Ā sß╗æ thß╗▒c, (sß╗æ 3 l├Ā sß╗æ hß╗»u tß╗Ę)
ŌćÆ Vß║Ły, sß╗æ 3 l├Ā sß╗æ thß╗▒c.
H├¼nh thß╗®c l├┤gic cß╗¦a luß║Łn ti├¬u kß║┐t Anxtß╗æt c├│ dß║Īng sau d├óy:
S l├Ā P1
P1 l├Ā P2
P2 l├Ā P3
Pn l├Ā Pn+1
Vß║Ły S l├Ā Pn+1











