Bài giảng Bài 1: Lý thuyết về sản xuất có nội dung trình bày về khái niệm của hàm sản xuất, hàm sản xuất ngắn hạn, dài hạn, công thức tính năng suất trung bình, năng suất biên, tổng sản lượng trong sản xuất ngắn hạn,... Mời các bạn tham khảo bài giảng để nắm rõ nội dung chi tiết.
Tóm tắt lý thuyết
1. Hàm sản xuất
Để tiến hành sản xuất sản phẩm cẩn có các yếu tố sản xuất như: nguyên, nhiên vật liệu, máy móc thiết bị, nhà xưởng, lao động,... Chúng được kết hợp với nhau theo một kỹ thuật nào đó để tạo thành sản phẩm.
Để diễn tả mối tương quan vật thể giữa sản lượng và các yếu tố sản xuất được sử dụng, người ta sử dụng hàm sản xuất.
- Hàm sản xuất mô tả những số lượng sản phẩm (đầu ra) tối đa có thể được sản xuất bởi một số lượng các yếu tố sản xuất (đầu vào) nhất định, tương ứng với trình độ kỹ thuật nhất định.
Dạng tổng quát của hàm sản xuất:
Q = f(X1,X2, X3,....................... Xn)
Với Q: số lượng sản phẩm đầu ra.
X : số lượng yếu tố sản xuất i.
Để đơn giản, ta chia các yếu tố sản xuất thành hai loại là vốn (K) và lao động (L), do đó hàm sản xuất có thể viết lại:
Q = f(K, L)
- Hàm sản xuất diễn tả số lượng tối đa sản phẩm được sản xuất, nghĩa là các doanh nghiệp sử dụng mọi phối hợp các yếu tố sản xuất một cách hiệu quả nhất, nó không để cập đến các trường hợp sản xuất kém hiệu quả.
- Hàm sản xuất cũng thể hiện mối quan hệ phụ thuộc giữa số lượng sản phẩm sản xuất với các yếu tố đầu vào nhất định. Một trong các yếu tố sản xuất thay đổi số lượng được sử dụng, sẽ dẫn đến sản lượng thay đổi theo.
- Kỹ thuật sản xuất thay đổi, thì hàm sản xuất sẽ thay đổi.
Để phân biệt tác động của việc thay đổi một yếu tố sản xuất và của tất cả yếu tố sản xuất đến sản lượng, ta phân biệt hàm sản xuất ngắn hạn và hàm sản xuất dài hạn.
- Hàm sản xuất ngắn hạn
Ngắn hạn là khoảng thời gian có ít nhát một yếu tổ sản xuất mà doanh nghiệp không thể thay đổi về số lượng sử dụng trong quá trình sản xuất.
Do đó, trong ngắn hạn các yếu tố sản xuất được chia làm hai loại:
- Yếu tố sản xuất cố định: không dễ dàng thay đổi trong quá trình sản xuất như: số lượng máy móc thiết bị, nhà xưởng, nhân viên quản trị tối cao... biểu thị cho quy mô sản xuất nhất định.
- Yếu tố sản xuất biến đổi: dễ dàng thay đổi về số lượng trong quá trình sản xuất như: nguyên, nhiên, vật liệu, lao động trực tiếp...
Như vậy, trong ngắn hạn quy mô sản xuất của doanh nghiệp là không đổi. Doanh nghiệp có thể thay đổi sản lượng ngắn hạn, bằng cách thay đổi số lượng yếu tố sản xuất biến đổi.
Trong ngắn hạn vốn (K) được coi là yếu tố sản xuất cố định và lao động (L) là yếu tố sản xuất biến đổi, hàm sản xuất trong ngắn hạn có dạng:
Q = f \((\overline{K} , L)\)
Với: K : Lượng vốn không đổi
L : Lượng lao động biến đổi
Q : Sản lượng được sản xuất ra
Trong ngắn hạn, vì vốn coi như không đổi nên sản lượng chỉ phụ thuộc vào mức sử dụng lao động. Do đó, hàm sản xuất ngắn hạn đơn giản là:Q = f(L)
- Hàm sản xuất dài hạn
Dài hạn là thời gian đủ dài để doanh nghiệp thay đổi tất cả các yếu tố sản xuất được sử dụng, mọi yếu tố sản xuất đều biến đổi.
Trong dài hạn doanh nghiệp có đủ thời giờ để thay đổi quy mô sản xuất theo ý muốn, do đó sản lượng trong dài hạn thay đổi nhiều hơn so với trong ngắn hạn.
Khi tất cả các yếu tố sản xuất đều biến đổi, ta có hàm sản xuất dài hạn: Q = f(K,L)
Trong dài hạn sản lượng phụ thuộc vào cả 2 yếu tố sản xuất biến đổi K và L.
2. Sản xuất trong ngắn hạn: có một yếu tố đầu vào thay đổi
Trong ngắn hạn, ta quan sát một yếu tố sản xuất biến đổi trong khi các yếu tố sản xuất còn lại được giữ nguyên thì sản lượng, năng suất trung bình và năng suất biên của yếu tố sản xuất biến đổi sẽ thay đổi khi số lượng yếu tố sản xuất thay đổi.
Trong ngắn hạn, chỉ có lao động (L) là yếu tố sản xuất biên đổi, còn vốn (K) được coi là yếu tố sản xuất cố định, thì sản lượng (Q) chỉ phụ thuộc vào L.
2.1 Tổng sản lượng trong ngắn hạn (Q)
Hàm sản xuất ngắn hạn đơn giản là: Q = f (L)
Sản lượng trong ngắn hạn có đặc điểm là lúc đầu khi gia tăng số lượng lao động được sử dụng, thì sản lượng tăng với tốc độ tăng dần, sau đó tốc độ tăng sản lượng giảm dần. Đến khi sản lượng đạt tối đa, nếu tiếp tục gia tăng số lượng lao động, thì sản lượng có thể giảm xuống:
- Ban đầu: L tăng thì Q tăng
- Sau đó: L tiếp tục tăng thì Qmax
- Nếu tiếp tục tăng L thì Q giảm
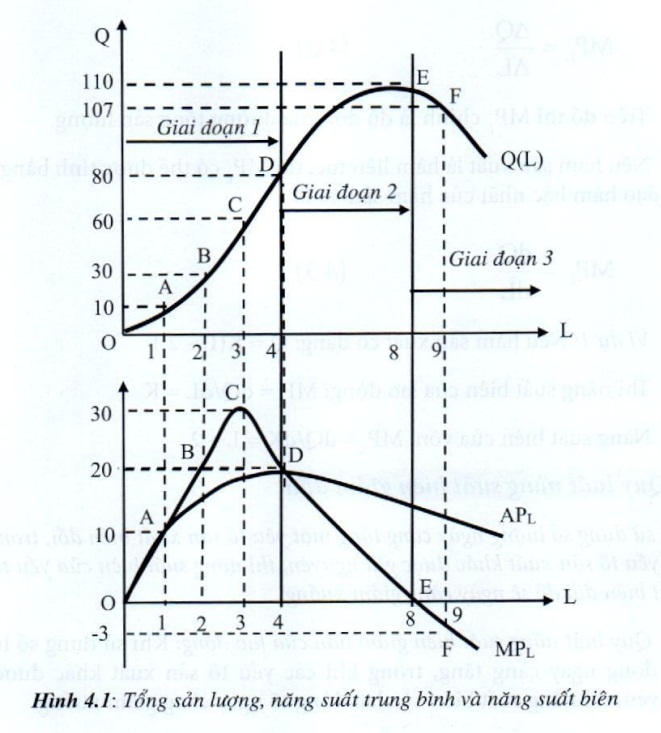
Trên đồ thị 4.1, khi tăng số lượng lao động đến L0= 3 thì sản lượng tăng nhanh dần, tiếp tục tăng số lượng lao động thì sản lượng tăng chậm dần và đạt cực đại tại L2 = 8. Sau đó tiếp tục tăng số lượng lao động thì sản lượng giảm dần.
2.2 Năng suất trung bình (AP)
- Năng suất trung bình của một yếu tố sản xuất biến đổi là số sản phẩm sản xuất tính trung bình trên một đơn vị yếu tố sản xuất đó.
Năng suất trung bình được xác định bằng cách lấy tổng sản lượng Q chia cho số lượng yếu tố sản xuất biến đổi được sử dụng.
Ví dụ: Năng suất trung bình của yếu tố lao động (AP[) là số sản phẩm tính trung bình cho mỗi lao động sản xuất ra:
\(AP_L = \frac{Q}{L}\) (4.1)
Năng suất trung bình của lao động có đặc điểm là:
- Ban đầu khi gia tăng lượng lao động sử dụng (L) thì APL tăng dần và đạt cực đại.
- Sau đó nếu tiếp tục gia tăng lao động thì APL giảm dần
Trên đồ thị 4.1, khi tăng số lượng lao động thì năng suất trung bình của lao động tăng dần và đạt cực đại tại I. = 4. Sau đó tiếp tục tăng số lượng lao động, thì năng suất trung bình sẽ giảm dần.
2.3 Năng suất biên
Năng suất biên của một yếu tố sản xuất biến đổi là phần thay đổi trong tổng sản lượng khi thay đổi một đơn vị yếu tố sản xuất biến đổi đó, trong khi các yếu tố sản xuất khác được giữ nguyên.
Năng suất biên của lao động (MPL) là phấn sản lượng tăng thêm trong tổng sản lượng khi sử dụng thêm một đơn vị lao động, khi các yếu tố sản xuất khác được giữ nguyên.
\(MP_L = \frac{\Delta Q}{\Delta L}\) (4.2)
Trên đồ thị MPL chính là độ dốc của đường tổng sản lượng.
Nếu hàm sản xuất là hàm liên tục, thì MPL có thể được tính bằng cách lấy đạo hàm bậc nhất của hàm sản xuất:
\(MP_L = \frac{dQ}{dL}\) (4.3)
Ví dụ 1: Nếu hàm sản xuất có dạng: Q = K(L - 2 )
Thì năng suất biên của lao động: MPL = dQ/dL = K
Năng suất biên của vốn: MPK= dQ/dK = L - 2
2.4 Quy luật năng suất biên giảm dần
- Khi sử dụng số lượng ngày càng tăng một yếu tố sản xuất biến đổi, trong khi các yếu tố sản xuất khác được giữ nguyên, thì năng suất biên của yếu tố sản xuất biến đổi đó sẽ ngày càng giảm xuống.
Quy luật năng suất biên giảm dần của lao động: Khi sử dụng số lượng lao động ngày càng tăng, trong khi các yếu tố sản xuất khác được giữ nguyên, thì năng suất biên của lao động sẽ ngày càng giảm xuống.
Ví dụ 2: Ta có hàm sản xuất ngắn hạn thể hiện qua bảng 4.1:
Bảng 4.1:
|
K |
L |
Q |
Ap. |
MP( |
Các giai đoạn sx |
|
10 |
0 |
0 |
/ |
/ |
GDI |
|
10 |
1 |
10 |
10,00 |
10 |
I |
|
10 |
2 |
30 |
15,00 |
20 |
I |
|
10 |
3 |
60 |
20,00 |
30 |
I |
|
10 |
4 |
80 |
20,00 |
20 |
GĐII |
|
10 |
5 |
95 |
19,00 |
15 |
II |
|
10 |
6 |
105 |
17,50 |
10 |
II |
|
10 |
7 |
110 |
15,70 |
5 |
II |
|
10 |
8 |
110 |
13,75 |
0 |
GĐIII |
|
10 |
9 |
107 |
11,88 |
-3 |
III |
|
10 |
10 |
100 |
10,00 |
-7 |
III |
Từ bảng 4.1, chúng ta có thể mô tả tổng sản lượng, năng suất trung bình và năng suất biên của yếu tố lao động bằng đồ thị 4.1 như sau:
2.5 Mối quan hệ giữa năng suất trung bình và năng suất biên
Năng suất trung bình và năng suất biên của yếu tố sản xuất biến đổi (như yếu tố lao động) có mối quan hệ mật thiết với nhau:
- Khi năng suất biên lớn hơn năng suất trung bình, thì năng suất trung bình tăng (MP > AP \(\rightarrow\) AP tăng)
- Khi năng suất biên nhỏ hơn năng suất trung bình, thì năng suất trung bình giảm (MP < AP \(\rightarrow\) AP giảm)
- Khi năng suất biên bằng năng suất trung bình, thì năng suất trung bình đạt CƯC đại (MP = AP \(\rightarrow\) AP max)
Ta có thể chứng minh mối quan hệ trên bằng phương pháp đại số:
\(AP_L = \frac{Q}{L}\)
Lấy đạo hàm cả hai về:
\(\frac{dAP}{dL} = \frac{dQ/L}{dL} = \frac{L \cdot \frac{dQ}{dL} - Q \cdot \frac{dL}{dL}}{L^2} = \frac{1}{L} (MP_L - AP_L)\)
- Khi \(MP_L > AP_L \implies \frac{dAP}{dL} > 0 \implies AP_L \uparrow\)
- Khi \(MP_L < AP_L \implies \frac{dAP}{dL} < 0 \implies AP_L \downarrow\)
- Khi \(MP_L = AP_L \implies \frac{dAP}{dL} = 0 \implies AP_L max\)
2.6 Mối quan hệ giữa năng suất biên và tổng sản lượng
Giữa năng suất biên và tổng sản lượng cũng có mối quan hệ mật thiết như sau:
- Khi năng suất biên còn dương thì tổng sản lượng còn tăng (khi MP > 0 \(\rightarrow\) Q tăng)
- Khi năng suất biên âm thì tổng sản lượng sẽ giảm (khi MP < 0 \(\rightarrow\) Q giảm)
- Khi năng suất biên bằng không thì tổng sản lượng đạt tối đa (khi MP = 0 \(\rightarrow\) Q max)
Qua 10 phối hợp khác nhau giữa K và L, ta nhận thấy có những phối hợp mang lại hiệu quả kinh tế, có những phối hợp không mang lại hiệu quả kinh tế. Vậy khi tiến hành sản xuất, người ta sẽ lựa chọn các phối hợp nào trong các phối hợp nêu trên? Để tiện xác định, ta chia 10 phối hợp trên thành 3 giai đoạn với các đặc điểm sau:
- Giai đoạn I (Từ L0 = 1 đến L1 = 4): thể hiện hiệu quả sử dụng lao động và vốn đều tăng, vì khi gia tăng số lượng lao động đến L1 = 4, năng suất trung bình tăng dần lên và đạt cực đại ở cuối giai đoạn 1 và đầu giai đoạn II; đồng thời sản lượng cũng liên tục tăng trong giai đoạn I.
- Giai đoạn II (từ L1= 4 đến L2 = 8): thể hiện hiệu quả sử dụng lao động giảm và hiệu quả sử dụng vốn tiếp tục tăng, vì khi tiếp tục gia tăng lao động đến L2 = 8, thì năng suất trung bình, năng suất biên đều giảm, nhưng năng suất biên vẫn còn dương, do đó tổng sản lượng vẫn tiếp tục tăng và đạt cực đại ở cuối giai đoạn II.
- Giai đoạn III (L > L2 = 8): thể hiện hiệu quả sử dụng lao động và vốn giảm, vì nếu tiếp tục gia tăng lao động vượt quá L, thì năng suất trung bình giảm, năng suất biên âm, do đó sản lượng giảm.
Qua 3 giai đọan sản xuất nêu trên, khi tiến hành sản xuất thì các doanh nghiệp chỉ chọn những phối hợp các yếu tố sản xuất thuộc giai đọan II, không chọn giai đọan I và giai đọan III. Vì trong giai đọan I hiệu quả sử dụng các yếu tố còn tăng chưa đạt tối đa, còn giai đọan III thì kém hiệu quả.
Trong giai đoạn II, phối hợp lao động và vốn đưa đến hiệu quả cao nhất vì hiệu quả sử dụng lao động cao nhất (APmax) ở đầu giai đoạn II, hiệu quả sử dụng vốn cao nhất (Qmax) ở cuối giai đoạn II (năng suất biên bằng không: MP = 0).











