Nội dung bài giảng Bài 4: Ma trận nghịch đảo sau đây sẽ giúp các bạn tìm hiểu về định lý, ma trận nghịch đảo, phương pháp tìm ma trận nghịch đảo, phương trình ma trận.
Tóm tắt lý thuyết
1. Định lý
Cho A, B là 2 ma trận vuông cùng cấp, ta có
det(A.B) = detA.detB
2. Ma trận nghịch đảo
Ma trận vuông A cấp n gọi là khả đảo (hay khả nghịch) nếu tồn tại ma trận vuông X cấp n sao cho:
\(AX=XA=I_n\)
Khi đó, X được gọi là ma trận nghịch đảo (hay ma trận đảo) của A, ký hiệu là \(A^{-1}\).
Với A,B là hai ma trận vuông cùng cấp, ta có :
\((i) (A^{-1})^{-1}=A \)
\((ii) (A^{t})^{-1}=(A^{-1})^{t} \)
\((iii) (AB)^{-1}=B^{-1}A^{-1}\)
A là ma trận khả nghịch, ta nói rằng A là một ma trận không suy biến.
3. Phương pháp tìm ma trận nghịch đảo.
Cho A là một ma trận vuông. Ta có hai phương pháp tìm ma trận nghịch đảo của A.
Cách 1 (dùng phép biến đổi sơ cấp):
Để tìm ma trận đảo, nếu có, của ma trận vuông A cấp ra, ta lập ma trận \((A|I_n)\) cấp n x 2n, trong đó \(I_n\) là ma trận đơn vị cấp n, rồi dùng phép biến đổi sơ cấp trên dòng đưa \((A|I_n)\) về dạng bậc thang thu gọn. Nếu ở dạng bậc thang thu gọn, A biến thành \(I_n\) thì \(I_n\) biến thành \(A^{-1}\). Nếu R(A) < n thì A không khả đảo.
Cách 2 (dùng định thức):
Nếu A không suy biến ta tìm nghịch đảo của A theo các bước sau:
Tính |A| .
Tìm ma trận các phần bù đại số của A:
\(\left( {{A_{{\rm{ij}}}}} \right) = \left( \begin{array}{l} {A_{11}} \cdots {A_{1n}}\\ \vdots \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\, \vdots \\ {A_{n1}} \cdots \,{A_{nn}} \end{array} \right)\)
Tìm ma trận phụ hợp, là chuyển vị của ma trận trên: Ký hiệu \(P_A=(A_{ij})^t\)
Tính ma trận nghịch đảo theo công thức:
\({A^{ - 1}} = \frac{1}{{\left| A \right|}}{\left( {{A_{{\rm{ij}}}}} \right)^t} = \frac{1}{{\left| A \right|}}{P_A}\)
Ví dụ: Tìm ma trận đảo của ma trận sau đây (nếu có)
\(A = \left( \begin{array}{l} 1\,\,\,\,2\,\,\,0\\ 2\,\,\,9\,\,\,1\,\\ 1\,\,\,1\,\,\,\,2 \end{array} \right)\)
Giải:
Cách 1:
Ta có:

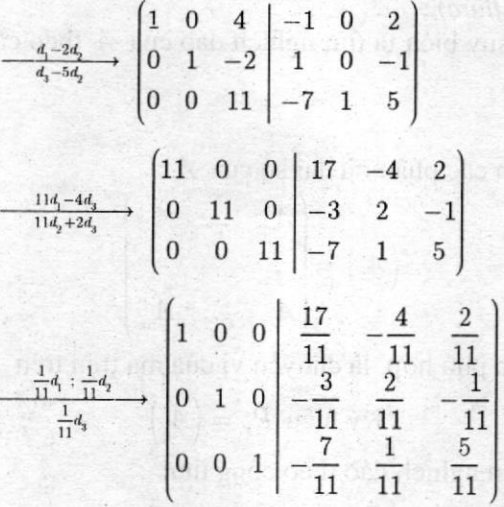
Vậy \({A^{ - 1}} = \left( {\begin{array}{*{20}{c}} {\frac{{17}}{{11}}}&{ - \frac{4}{{11}}}&{\frac{2}{{11}}}\\ { - \frac{3}{{11}}}&{\frac{2}{{11}}}&{ - \frac{1}{{11}}}\\ { - \frac{7}{{11}}}&{\frac{1}{{11}}}&{\frac{5}{{11}}} \end{array}} \right)\)
Cách 2:
Ta có \(\left| A \right| = 11 \ne 0\)
Ma trận phụ hợp của A là: \({P_A} = \left( {\begin{array}{*{20}{c}} {17}&{ - 4}&2\\ { - 3}&2&{ - 1}\\ { - 7}&1&5 \end{array}} \right)\)
Do đó ma trận nghịch đảo của A là
\({A^{ - 1}} = \frac{1}{{\left| A \right|}}{P_A} = \frac{1}{{11}}\left( {\begin{array}{*{20}{c}} {17}&{ - 4}&2\\ { - 3}&2&{ - 1}\\ { - 7}&1&5 \end{array}} \right)\)
Vi dụ: Tìm ma trận đảo (nếu có) của ma trận \(A = \left( {\begin{array}{*{20}{c}} 2&1&3\\ 3&1&2\\ 1&0&{ - 1} \end{array}} \right)\)
Giải
Vì |A| = 0 nên A là ma trận không khả nghịch.
4. Phương trình ma trận.
(i) Với A khả đảo:
\(\begin{array}{l} {A_{n\,x\,m}}{X_{n\,x\,k}} = {B_{n\,x\,k}} \Leftrightarrow {A^{ - 1}}{\rm{(AX}}) = {A^{ - 1}}B\\ \Leftrightarrow ({A^{ - 1}}A)X = {A^{ - 1}}B \Leftrightarrow {I_n}X = {A^{ - 1}}B\\ \Leftrightarrow X = {A^{ - 1}}B \end{array}\)
(ii) Với A khả đảo :
\(\begin{array}{l} {X_{n\,x\,k}}{A_{n\,x\,m}} = {B_{n\,x\,k}} \Leftrightarrow {\rm{(XA}}){A^{ - 1}} = B{A^{ - 1}}\\ \Leftrightarrow X(A{A^{ - 1}}) = B{A^{ - 1}} \Leftrightarrow X{I_n} = B{A^{ - 1}}\\ \Leftrightarrow X = B{A^{ - 1}} \end{array}\)
(iii) Với A, B khả đảo:
\({\begin{array}{*{20}{l}} {{A_{m{\kern 1pt} x{\kern 1pt} m}}{X_{m{\kern 1pt} x{\kern 1pt} n}}{B_{n{\kern 1pt} x{\kern 1pt} n}} = {C_{m\,\,x\,n}} \Leftrightarrow {A^{ - 1}}({\rm{AXB}}){B^{ - 1}} = {A^{ - 1}}CB}\\ \begin{array}{l} \Leftrightarrow ({A^{ - 1}}A)X(B{B^{ - 1}}) = {A^{ - 1}}C{B^{ - 1}}\\ \Leftrightarrow {I_m}X{I_n} = {A^{ - 1}}C{B^{ - 1}} \Leftrightarrow X = {A^{ - 1}}C{B^{ - 1}} \end{array}\\ {} \end{array}^{ - 1}}\)
Ví dụ : Tìm ma trận X thỏa XA = B với
\(A = \left( {\begin{array}{*{20}{c}} 1&{\,\,0}&2\\ 2&{ - 1}&3\\ 4&1&8 \end{array}} \right)\) và \(B = \left( {\begin{array}{*{20}{c}} 1&{\,\, - 2}&{ - 1}\\ 2&1&3\\ \begin{array}{l} 0\\ 0 \end{array}&\begin{array}{l} - 1\\ 1 \end{array}&\begin{array}{l} 2\\ 3 \end{array} \end{array}} \right)\)
Giải
Ta có:
\((A|I) = \left( {\begin{array}{*{20}{c}} 1&{{\mkern 1mu} {\mkern 1mu} 0}&2\\ 2&{ - 1}&3\\ 4&1&8 \end{array}\left| {\begin{array}{*{20}{c}} 1&{{\mkern 1mu} {\mkern 1mu} 0}&0\\ 0&1&0\\ 0&0&1 \end{array}} \right.} \right)\)


Vậy \({A^{ - 1}} = \left( {\begin{array}{*{20}{c}} { - 11}&{{\mkern 1mu} {\mkern 1mu} 2}&2\\ { - 4}&0&1\\ 6&{ - 1}&{ - 1} \end{array}} \right)\)
Do đó \(X = B{A^{ - 1}} = \left( {\begin{array}{*{20}{c}} 1&{{\mkern 1mu} {\mkern 1mu} - 2}&{ - 1}\\ 2&1&3\\ \begin{array}{l} 0\\ 0 \end{array}&\begin{array}{l} - 1\\ 1 \end{array}&\begin{array}{l} 2\\ 3 \end{array} \end{array}} \right)\left( {\begin{array}{*{20}{c}} { - 11}&{{\mkern 1mu} {\mkern 1mu} 2}&2\\ { - 4}&0&3\\ 6&{ - 1}&{ - 1} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - 9}&{{\mkern 1mu} {\mkern 1mu} 3}&1\\ { - 8}&1&2\\ \begin{array}{l} 16\\ 14 \end{array}&\begin{array}{l} - 2\\ - 3 \end{array}&\begin{array}{l} - 3\\ - 2 \end{array} \end{array}} \right)\)










