Mời các bạn cùng tham khảo nội dung bài giảng Bài 2: Định thức sau đây để tìm hiểu về định thức của ma trận vuông cấp 1, phần bù đại số, định thức của ma trận vuông cấp n >2.
Tóm tắt lý thuyết
1. Định thức của ma trận vuông cấp 1
Cho \(A = {\left( a \right)_{1x1}}\) là ma trận vuông cấp 1. Ta định nghĩa định thức của A như sau: |A| = |a| = a (cần phân biệt với ký hiệu trị tuyệt đối)
Ví dụ: A = (-3), |A| = |(-3)| = -3
2. Phần bù đại số
Với \(A = {\left( {{a_{\rm{i}}}_{\rm{j}}} \right)_{nxn}},(n = 2,3,...)\)ta định nghĩa định thức con Mij bù của phần tử aij là định thức của ma trận vuông có được bằng cách bỏ đi dòng thứ i và cột thứ j của A. Phần bù đại số của phần tử aij được định nghĩa bởi:
\({A_{{\rm{ij}}}} = {( - 1)^{i + j}}\,{M_{{\rm{ij}}}}\)
Ví dụ: Với \(A = \left( \begin{array}{l} 1\,\,\,\, - 2\\ 3\,\,\,\,\,\,\,\,5 \end{array} \right)\), ta có:
M21 = -2, M12 = 3
\(\begin{array}{l} {A_{21}} = {( - 1)^{2 + 1}}{M_{21}} = 2\\ {A_{12}} = {( - 1)^{1 + 2}}{M_{12}} = - 3 \end{array}\)
3. Định thức của ma trận vuông cấp n \(\ge 2\)
Với ma trận \(A = {\left( {{\rm{aij}}} \right)_{nxm}},(n = 2,3,...)\)ta định nghĩa định thức của A như sau:
\(\det \,A = \left| A \right| = {a_{{\rm{ij}}}}{A_{i1}} + {a_{{\rm{i2}}}}{A_{i2}} + ... + {a_{{\rm{in}}}}{A_{in}},i = 1,...n\)(khai triển theo dòng thứ i)
hoặc
\(\left| A \right| = {a_{1j}}{A_{1j}} + {a_{2j}}{A_{2j}} + ... + {a_{nj}}{A_{nj}},j = 1,...n\) (khai triển theo cột thứ j)
Ví dụ: Tính \(\left| A \right| = \left| \begin{array}{l} {a_{11}}\,\,\,{a_{12}}\\ {a_{21}}\,\,\,{a_{22}}\, \end{array} \right|\) bằng cách khai triển theo dòng hoặc cột.
Giải
Ta có
Khai triển theo dòng 1:
\(\left| A \right| = {a_{11}}\left| {({a_{22}})} \right| - {a_{12}}\left| {({a_{21}})} \right| = {a_{11}}{a_{22}} - {a_{12}}{a_{21}}\)
Khai triển theo dòng 2:
\(\left| A \right| = - {a_{21}}\left| {({a_{12}})} \right| + {a_{22}}\left| {({a_{11}})} \right| = {a_{11}}{a_{22}} - {a_{12}}{a_{21}}\)
Khai trển theo cột 1:
\(\left| A \right| = {a_{11}}\left| {({a_{22}})} \right| - {a_{21}}\left| {({a_{12}})} \right| = {a_{11}}{a_{22}} - {a_{12}}{a_{21}}\)
Khai triển theo cột 2:
\(\left| A \right| = - {a_{12}}\left| {({a_{21}})} \right| + {a_{22}}\left| {({a_{11}})} \right| = {a_{11}}{a_{22}} - {a_{12}}{a_{21}}\)
Tóm lại ta có:
\(\left| \begin{array}{l} {a_{11}}\,\,\,{a_{12}}\\ {a_{21}}\,\,\,{a_{22}} \end{array} \right| = {a_{11}}{a_{22}} - {a_{12}}{a_{21}}\)
Ví dụ: Tính \(\left| \begin{array}{l} 2\,\,\, - 5\\ 3\,\,\,\,\,\,\,1 \end{array} \right| = 2.1 - 3.( - 5) = 17\)
Ví dụ: Tính \(\left| A \right| = \left| \begin{array}{l} {a_{11}}\,\,\,{a_{12}}\,\,\,{a_{13}}\\ {a_{21}}\,\,\,{a_{22}}\,\,\,{a_{23}}\\ {a_{31}}\,\,\,{a_{31}}\,\,\,{a_{33}}\, \end{array} \right|\) bằng cách khai triển theo dòng 2
Ta có:
\(\left| A \right| = {a_{21}}{A_{21}} + {a_{22}}{A_{22}} + {a_{23}}{A_{23}}\)
\(= - {a_{21}}\left| \begin{array}{l} {a_{12}}\,\,\,\,{a_{13}}\\ {a_{32}}\,\,\,\,{a_{33}} \end{array} \right| + {a_{22}}\left| \begin{array}{l} {a_{11}}\,\,\,\,{a_{13}}\\ {a_{31}}\,\,\,\,{a_{33}} \end{array} \right| - {a_{23}}\left| \begin{array}{l} {a_{11}}\,\,\,\,{a_{12}}\\ {a_{31}}\,\,\,\,{a_{32}} \end{array} \right|\)
\(= ({a_{11}}{a_{22}}{a_{33}} + {a_{12}}{a_{23}}{a_{31}} + {a_{21}}{a_{32}}{a_{11}}) + ({a_{13}}{a_{22}}{a_{31}} + {a_{21}}{a_{12}}{a_{33}} + {a_{11}}{a_{23}}{a_{32}})\)
Người ta có thể dùng quy tắc Sarrus để biểu diễn kết quả trên như sau:
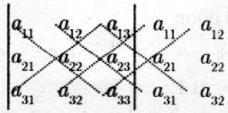
= tổng các tính số từ trái sang phải - tổng tích tích số từ phải sang trái.
Ví dụ: Tính định thức của \(A = \left( \begin{array}{l} 1\,\,\,\,\,\, - 2\,\,\,\,\,\,5\\ - 3\,\,\,\,\,\,0\,\,\,\,\,\,1\\ 2\,\,\,\,\,\,4\,\,\,\,\,\,3 \end{array} \right)\)
Áp dụng quy tắc Sarrus ta có:
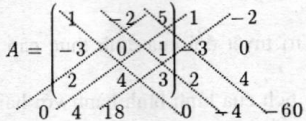
Nên \(\left| A \right| = (0 + ( - 4) + ( - 60) - (0 + 4 + 18) = - 86\)
Ví dụ: Tính định thức của ma trận
\(A = \left( \begin{array}{l} 1\,\,\,\,\,\,\,0\,\,\,\,\,0\,\,\,\,\,\,3\\ 2\,\, - 1\,\,\,\,\,1\,\,\,\,\, - 2\\ 1\,\,\,\,\,3\,\,\,\,\,\,\,1\,\,\,\,\,\,\,0\\ 2\,\,\,4\,\,\, - 2\,\,\,\,\,\,\,1 \end{array} \right)\)
Giải
Khai triển theo dòng 1 ta có:
\(\left| A \right| = {a_{11}}{A_{11}} + {a_{12}}{A_{12}} + {a_{13}}{A_{13}} + {a_{14}}{A_{14}}\)
\( = 1\left| \begin{array}{l} - 1\,\,\,\,1\,\,\,\, - 2\\ 3\,\,\,\,\,\,\,1\,\,\,\,\,\,\,\,0\\ 4\,\,\,\, - 2\,\,\,\,\,\,1 \end{array} \right| - 3\left| \begin{array}{l} 2\,\,\,\, - 1\,\,\,\,\,\,\,\,\,1\\ 1\,\,\,\,\,\,\,3\,\,\,\,\,\,\,\,\,\,1\\ 2\,\,\,\,\,\,\,4\,\,\,\, - 2 \end{array} \right|\)
\(= \left[ {( - 1 + 0 + 12) - ( - 8 + 3 + 0)} \right] - 3\left[ {( - 12 - 2 + 4) - (6 + 2 + 8)} \right] = 94\)
Nhận xét:
- Giá trị tuyệt đối của định thức cấp một \(\left| {(a)} \right|\) cho ta độn dài của vecto một chiều a.
Ví dụ: \(\left| {( - 2)} \right| = 2\)
- Giá trị tuyệt đối của định thức cấp 2 \(2\left| \begin{array}{l} {a_{11}}\,\,\,\,{a_{12}}\\ {a_{21}}\,\,\,\,{a_{22}} \end{array} \right|\) cho ta diện tích của hình bình hành với hai cạnh là các vecto \(({a_{11}};{a_{12}});({a_{21}};{a_{22}})\)
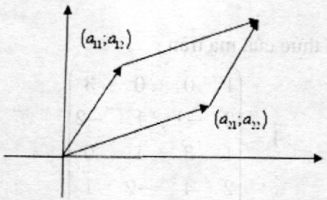
Ví dụ: Tính diện tích tam giác OAB với A(1;2); B(3;-2)
Giải
Ta có \({S_{\Delta ABC}} = \frac{1}{2}\left\| \begin{array}{l} 2\,\,\,1\\ 4\,\,\,2 \end{array} \right\| = 0\) vì \(\overrightarrow {OA} \) cùng phương với \(\overrightarrow {OB}\), nghĩa là hai vecto \(\overrightarrow {OA}\) và \(\overrightarrow {OB}\) phụ thuộc tuyến tính.










