-
Câu hỏi:
Thiết diện của 1 tứ diện có thể là:
- A. Tam giác
- B. Tứ giác
- C. Ngũ giác
- D. Tam giác hoặc tứ giác
Lời giải tham khảo:
Đáp án đúng: D
Đáp án: D
Giải thích:
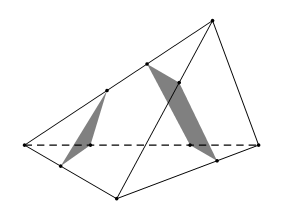
Khi thiết diện cắt 3 mặt của tứ diện thì sẽ tạo thành 3 giao tuyến. Ba giao tuyến lập thành 1 hình tam giác.
Khi thiết diện cắt cả 4 mặt của tứ diện thì sẽ tạo thành 4 giao tuyến. Bốn giao tuyến lập thành 1 hình tứ giác.
Thiết diện không thể là ngũ giác vì thiết diện có 4 mặt, số giao tuyến tối đa là 4.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Trong các khẳng định sau, khẳng định nào đúng? Qua 2 điểm phân biệt có duy nhất một mặt phẳng; ...
- Trong không gian, cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
- Cho tứ diện ABCD. Gọi E, F, G là các điểm lần lượt thuộc các cạnh AB, AC, BD sao cho EF cắt BC tại I, EG cắt AD tại H. Ba đường thẳng nào sau đây đồng quy?
- Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
- Trong các mệnh đề sau đây, mệnh đề nào sai? Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa
- Cho 3 đường thẳng \(d_1,d_2,d_3\) không cùng thuộc một mặt phẳng và cắt nhau từng đôi. Khẳng định nào sau đây đúng?
- Thiết diện của 1 tứ diện có thể là:
- Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC, E là điểm trên cạnh CD với ED=3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là:
- Cho tứ diện ABCD. Gọi H, K lần lượt là trung điểm các cạnh AB, BC. Trên đường thẳng CD lấy điểm M nằm ngoài đoạn CD. Thiết diện của tứ diện với mặt phẳng (HKM) là:
- Cho 3 điểm không thẳng hàng. số mặt phẳng phân biệt đi qua ba điểm đó là:







