-
Câu hỏi:
Cho tứ diện ABCD có các cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó thiết diện của hình tứ diện cắt bởi mp qua M và song song với mp(ACD) là:
- A. \(\frac{{{\left( a+m \right)}^{2}}\sqrt{3}}{4}\)
- B. \(\frac{{{\left( a-m \right)}^{2}}\sqrt{3}}{4}\)
- C. \(\frac{{{\left( a-m \right)}^{2}}\sqrt{2}}{2}\)
- D. \(\frac{{{m}^{2}}\sqrt{3}}{4}\)
Lời giải tham khảo:
Đáp án đúng: B
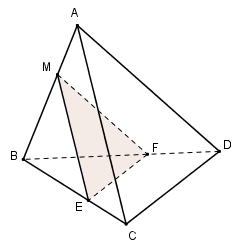
Trong (ABC) qua M kẻ đường thẳng song song với AC cắt BC tại E \(\Rightarrow \left( \alpha \right)\cap \left( ABC \right)=ME\).
Trong (ABD) qua M kẻ đường thẳng song song với AD cắt BD tại F \(\Rightarrow \left( \alpha \right)\cap \left( ABD \right)=MF.\)
\(\Rightarrow \left( \alpha \right)\cap \left( BCD \right)=EF.\)
Vậy thiết diện cần tìm là tam giác MEF.
Ta có: \(ME\parallel CD\Rightarrow \frac{ME}{CD}=\frac{BM}{AB}\Leftrightarrow \frac{ME}{a}=\frac{a-m}{a}\Leftrightarrow ME=a-m.\)
\(\text{EF}\parallel CD\Rightarrow \frac{EF}{CD}=\frac{BE}{BC}=\frac{ME}{AC}\Leftrightarrow \frac{EF}{a}=\frac{a-m}{a}\Rightarrow EF=a-m\).
Chứng minh tương tự ta có MF = a – m.. Suy ra tam giác MEF đều cạnh a – m.
Vậy \({{S}_{MEF}}=\frac{{{\left( a-m \right)}^{2}}\sqrt{3}}{4}.\)
Chọn B.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Tìm ảnh của\((d):2x+3y-1=0\) qua phép tịnh tiến theo \(\vec{v}=(2;5)\)
- Cho 6 chữ số 2, 3, 4, 5, 6, 7. Hỏi có bao nhiêu số gồm 3 chữ số được lập thành từ 6 chữ số đó:
- Trong không gian, xét vị trí tương đối của đường thẳng với mặt phẳng thì số khả năng xãy ra tối đa là:
- Giải phương trình \(\cos 2x-5\sin x-3=0\) ta được nghiệm là:
- Cho hình tứ diện ABCD. Tổng số đỉnh và số cạnh của hình tứ diện bằng:
- Cho tứ diện ABCD có các cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó thiết diện của hình tứ diện cắt bởi mp qua M và song song với mp(ACD) là:
- Tính tổng \(S=1.2+2.3+.\text{ }.\text{ }.+(n-2)(n-1)+(n-1)n\) với mọi \(n\ge 2\)
- Cho hình chóp S.ABCD, đáy là hình thang, đáy lớn AB, giao tuyến của mặt (SAD) và (SBC) là:
- Gọi (d) là ảnh của đường thẳng \((\Delta ):x-y+1=0\) qua phép tịnh tiến theo \(\overrightarrow{a}=(1;1)\). Tọa độ giao điểm M của (d) và \(({{d}_{1}}):2x-y+3=0\) là?
- Trong mặt phẳng \(Oxy\) cho đường tròn \(\left( C \right):{{\left( x-2 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=4\). Hỏi phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số \(k=\frac{1}{2}\) và phép quay tâm O góc 900 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau:
- Trong mp Oxy, cho 2 điểm A(2;-4), B(1;0), phép tịnh tiến theo \(\overrightarrow{OA}\) biến điểm B thành B’ , khi đó B’ có tọa độ là:
- Cho cấp số cộng \(\left( {{u}_{n}} \right)\) biết \({{u}_{1}}=7\) và \(d=4\). Lựa chọn kết quả đúng trong các kết quả sau:
- Từ tập X = {0;1;2;3;4;5} có thể lập được bao nhiêu số tự nhiên gồm ba chữ số khác nhau mà số đó chia hết cho 10.
- Điều kiện để phương trình sau \(m\sin x+8\cos x=10\) vô nghiệm là
- Viết phương trình (C') là ảnh của (C):\({{(x-2)}^{2}}+{{(y+3)}^{2}}=16\) qua phép tịnh tiến theo \(\vec{v}=(1;-2)\).
- Phương trình \(1+2\cos 2x=0\) có nghiệm \(\left( k\in Z \right)\)
- Cho hình chóp S,ABCD có đáy ABCD là một tứ giác (AB không song song với CD). Gọi M là trung điểm của SD, N là điểm nằm trên cạnh SB sao cho \(SN=2NB\), O là giao điểm của AC và BD. Cặp đường thẳng nào sau đây cắt nhau:
- Hỏi trong các khẳng định sau khẳng định nào sai ?
- Cho dãy số \(\left( {{u_n}} \right)\) với \({{u}_{n}}=\frac{n-1}{{{n}^{2}}+1}\) ; biết \({{u}_{k}}=\frac{2}{13}\) . \({{u}_{k}}\)là số hạng thứ mấy của dãy số đã cho?
- Phép vị tự tâm \(O(0;0)\) tỉ số \(k=-2\) biến đường tròn: \(\left( C \right):\,\,{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=4\) thành đường nào?
- Với giá trị nào của tham số m thì phương trình \(\sin x+3-m=0\) có nghiệm.
- Cho \(A = \left\{ {0;1;2;3;4;5} \right\}\). Từ tập A có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau chia hết cho 3?
- Cho hình chóp S.ABCD có đáy ABCD là hình bình hành thì giao tuyến của (SAD) và (SBC) là:
- Trong mặt phẳng Oxy cho \(M\left( 0;2 \right),N\left( -2;1 \right),\overrightarrow{v}=\left( 1;2 \right)\). Ảnh của M, N qua T\(_{\overrightarrow{v}}\) lần lượt biến thành M’, N’ thì độ dài M’N’ là:
- Phương trình lượng giác: \({{\cos }^{2}}\,x+2\cos x-3=0\) có nghiệm là\(\left( k\in Z \right)\):
- Cho cấp số cộng \(\left( {{u}_{n}} \right):10;\,\,a;\,\,4;\,\,b\) thì giá trị của \(a,b\) là:
- Chọn dãy số tăng trong các dãy số có số hạng tổng quát sau đây:
- Cho hình chóp S.ABCD, gọi M là trung điểm AB, mặt phẳng \(\left( \alpha \right)\) qua M song song với SB và AD. Hỏi thiết diện tạo bởi \(\left( \alpha \right)\) và hình chóp S.ABCD là hình gì?
- Từ các chữ số \(1,2,3,4,5,6,7,8,9\) có thể lập được bao nhiêu số tự nhiên gồm năm chữ số đôi một khác nhau và lớn hơn \(50000\).
- Một câu lạc bộ có 25 thành viên. Số cách chọn một ban quản lí gồm 1 chủ tịch, 1 phó chủ tịch và một thư ký là:
- Một tổ gồm có 6 học sinh nam và 5 học sinh nữ. Chọn từ đó ra 3 học sinh đi làm vệ sinh. Có bao nhiêu cách chọn trong đó có ít nhất một học sinh nam.
- Cho biết hình chóp S.ABCD, đáy là hình thang, đáy lớn AB, Gọi O là giao của AC với BD. M là trung điểm SC.
- Hệ số của \({{x}^{5}}\) trong khai triển \({{(1-x)}^{12}}\) là?
- Cho dãy số \(\left( {{u}_{n}} \right)\) biết \({{u}_{1}}=2\), \({{u}_{n+1}}={{u}_{n}}+1,\,\,\,\forall n\ge 1\). Lựa chọn phương án đúng trong các phương án sau:
- Số nghiệm của phương trình \(\sqrt{3}\tan \left( x+\frac{\pi }{3} \right)=1\) thuộc đoạn \(\left[ -\pi ;2\pi \right]\) là:
- Hỏi trong các hệ thức sau hệ thức nào sai?
- Trong mp Oxy, cho đường thẳng d : y = 3x. Ảnh của d qua phép quay tâm O góc quay a = 90o
- Cho cấp số cộng \(\left( {{u}_{n}} \right):-1;\,\,2;\,\,5;\,\,8;...\)Chọn khẳng định sai trong các khẳng định sau:
- Cho biết hai đường thẳng a và b. Điều kiện nào sau đây đủ để kết luận a và b chéo nhau?
- Cho biết tứ diện ABCD, M là trung điểm của AB, N là trung điểm của AC, P là trung điểm của AD.







